Morphological skeleton

In digital image processing, morphological skeleton is a skeleton (or medial axis) representation of a shape or binary image, computed by means of morphological operators.

Morphological skeletons are of two kinds:

Those defined by means of morphological openings, from which the original shape can be reconstructed,
Those computed by means of the hit-or-miss transform, which preserve the shape's topology.

Skeleton by openings

Lantuéjoul's formula

Continuous images

In (Lantuéjoul 1977),^[1] Lantuéjoul derived the following morphological formula for the skeleton of a continuous binary image 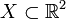$X\subset \mathbb{R}^2$ :

S(X)=\bigcup_{\rho >0}\bigcap_{\mu >0}\left[(X\ominus \rho B)-(X\ominus \rho B)\circ \mu \overline B\right]

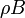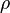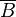where $\ominus$ and $\circ$ are the morphological erosion and opening, respectively, $\rho B$ is an open ball of radius $\rho$ , and $\overline B$ is the closure of $B$ .

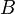Discrete images

Let 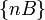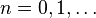$\{nB\}$ , $n=0,1,\ldots$ , be a family of shapes, where B is a structuring element,

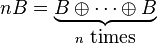nB=\underbrace{B\oplus\cdots\oplus B}_{n\mbox{ times}}

, and

0B=\{o\}

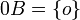, where o denotes the origin.

The variable n is called the size of the structuring element.

Lantuéjoul's formula has been discretized as follows. For a discrete binary image 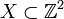$X\subset \mathbb{Z}^2$ , the skeleton S(X) is the union of the skeleton subsets 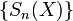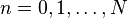$\{S_n(X)\}$ , $n=0,1,\ldots,N$ , where:

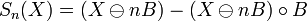S_n(X)=(X\ominus nB)-(X\ominus nB)\circ B

Reconstruction from the skeleton

The original shape X can be reconstructed from the set of skeleton subsets 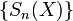$\{S_n(X)\}$ as follows:

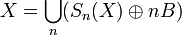X=\bigcup_n (S_n(X)\oplus nB)

Partial reconstructions can also be performed, leading to opened versions of the original shape:

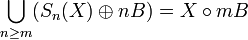\bigcup_{n\geq m} (S_n(X)\oplus nB)=X\circ mB

The skeleton as the centers of the maximal disks

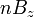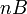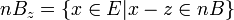Let $nB_z$ be the translated version of $nB$ to the point z, that is, $nB_z=\{x\in E| x-z\in nB\}$ .

A shape 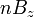$nB_z$ centered at z is called a maximal disk in a set A when:

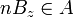$nB_z\in A$ , and
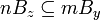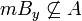if, for some integer m and some point y, $nB_z\subseteq mB_y$ , then $mB_y\not\subseteq A$ .

Each skeleton subset 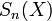$S_n(X)$ consists of the centers of all maximal disks of size n.

Notes

↑ See also (Serra's 1982 book)

References

Image Analysis and Mathematical Morphology by Jean Serra, ISBN 0-12-637240-3 (1982)
Image Analysis and Mathematical Morphology, Volume 2: Theoretical Advances by Jean Serra, ISBN 0-12-637241-1 (1988)
An Introduction to Morphological Image Processing by Edward R. Dougherty, ISBN 0-8194-0845-X (1992)
Ch. Lantuéjoul, "Sur le modèle de Johnson-Mehl généralisé", Internal report of the Centre de Morph. Math., Fontainebleau, France, 1977.