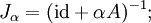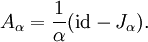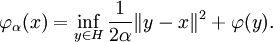Moreau's theorem
In mathematics, Moreau's theorem is a result in convex analysis. It shows that sufficiently well-behaved convex functionals on Hilbert spaces are differentiable and the derivative is well-approximated by the so-called Yosida approximation, which is defined in terms of the resolvent operator.
Statement of the theorem
Let H be a Hilbert space and let φ : H → R ∪ {+∞} be a proper, convex and lower semi-continuous extended real-valued functional on H. Let A stand for ∂φ, the subderivative of φ; for α > 0 let Jα denote the resolvent:
and let Aα denote the Yosida approximation to A:
For each α > 0 and x ∈ H, let
Then
and φα is convex and Fréchet differentiable with derivative dφα = Aα. Also, for each x ∈ H (pointwise), φα(x) converges upwards to φ(x) as α → 0.