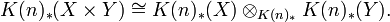Morava K-theory

In stable homotopy theory, a branch of mathematics, Morava K-theory is one of a collection of cohomology theories introduced in algebraic topology by Jack Morava in unpublished preprints in the early 1970s. For every prime number p (which is suppressed in the notation), it consists of theories K(n) for each nonnegative integer n, each a ring spectrum in the sense of homotopy theory. Johnson & Wilson (1975) published the first account of the theories.

Details

The theory K(0) agrees with singular homology with rational coefficients, whereas K(1) is a summand of mod-p complex K-theory. The theory K(n) has coefficient ring

F_p[v_n,v_n⁻¹]

where v_n has degree 2(pⁿ − 1). In particular, Morava K-theory is periodic with this period, in much the same way that complex K-theory has period 2.

These theories have several remarkable properties.

They have Künneth isomorphisms for arbitrary pairs of spaces: that is, for X and Y CW complexes, we have

K(n)_*(X \times Y) \cong K(n)_*(X) \otimes_{K(n)_*} K(n)_*(Y).

They are "fields" in the category of ring spectra. In other words every module spectrum over K(n) is free, i.e. a wedge of suspensions of K(n).
They are complex oriented (at least after being periodified by taking the wedge sum of (pⁿ − 1) shifted copies), and the formal group they define has height n.
Every finite p-local spectrum X has the property that K(n)_∗(X) = 0 if and only if n is less than a certain number N, called the type of the spectrum X. By a theorem of Devinatz–Hopkins–Smith, every thick subcategory of the category of finite p-local spectra is the subcategory of type-n spectra for some n.

References

Johnson, David Copeland; Wilson, W. Stephen (1975), "BP operations and Morava's extraordinary K-theories.", Math. Z. 144 (1): 55−75, doi:10.1007/BF01214408, MR 0377856
Hovey-Strickland, "Morava K-theory and localisation"
Ravenel, Douglas C. (1992), Nilpotence and periodicity in stable homotopy theory, Annals of Mathematics Studies 128, Princeton University Press, MR 1192553
Würgler, Urs (1991), "Morava K-theories: a survey", Algebraic topology Poznan 1989, Lecture Notes in Math. 1474, Berlin: Springer, pp. 111 138, doi:10.1007/BFb0084741, ISBN 978-3-540-54098-4, MR 1133896