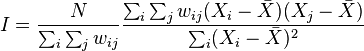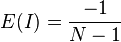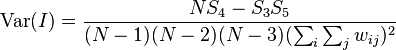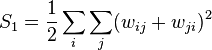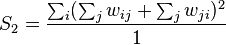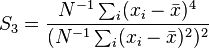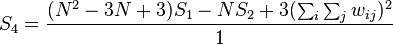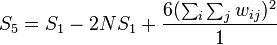Moran's I

In statistics, Moran's I is a measure of spatial autocorrelation developed by Patrick Alfred Pierce Moran.[1][2] Spatial autocorrelation is characterized by a correlation in a signal among nearby locations in space. Spatial autocorrelation is more complex than one-dimensional autocorrelation because spatial correlation is multi-dimensional (i.e. 2 or 3 dimensions of space) and multi-directional.
Definition
Moran's I is defined as
where 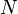 is the number of spatial units indexed by
is the number of spatial units indexed by 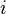 and
and 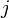 ;
;  is the variable of interest;
is the variable of interest; 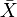 is the mean of
is the mean of  ; and
; and 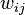 is an element of a matrix of spatial weights.
is an element of a matrix of spatial weights.
The expected value of Moran's I under the null hypothesis of no spatial autocorrelation is
Its variance equals
where
Negative values indicate negative spatial autocorrelation and the inverse for positive values. Values range from −1 (indicating perfect dispersion) to +1 (perfect correlation). A zero value indicates a random spatial pattern. For statistical hypothesis testing, Moran's I values can be transformed to Z-scores in which values greater than 1.96 or smaller than −1.96 indicate spatial autocorrelation that is significant at the 5% level.
Moran's I is inversely related to Geary's C, but it is not identical. Moran's I is a measure of global spatial autocorrelation, while Geary's C is more sensitive to local spatial autocorrelation.
Uses
Moran's I values is widely used in the analysis of geographic differences in health variables.[3] It has been used to characterize the impact of lithium concentrations in public water on mental health.[4] It has also recently been used in dialectology to measure the significance of regional language variation.[5]
Sources
- ↑ Moran, P. A. P. (1950). "Notes on Continuous Stochastic Phenomena". Biometrika 37 (1): 17–23. doi:10.2307/2332142. JSTOR 2332142.
- ↑ Li, Hongfei; Calder, Catherine A.; Cressie, Noel (2007). "Beyond Moran's I: Testing for Spatial Dependence Based on the Spatial Autoregressive Model". Geographical Analysis 39 (4): 357–375. doi:10.1111/j.1538-4632.2007.00708.x.
- ↑ "The Analysis of Spatial Association by Use of Distance Statistics". Geographical Analysis 24 (3): 189–206. 3 Sep 2010. doi:10.1111/j.1538-4632.1992.tb00261.x.
- ↑ "Geospatial examination of lithium in drinking water and suicide mortality". Int J Health Geogr. 11 (1): 19. 2012. doi:10.1186/1476-072X-11-19.
- ↑ Grieve, Jack (2011). "A regional analysis of contraction rate in written Standard American English". International Journal of Corpus Linguistics 16 (4): 514–546. doi:10.1075/ijcl.16.4.04gri.