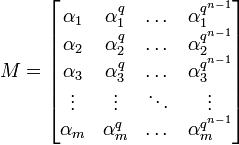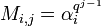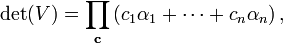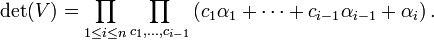Moore matrix
In linear algebra, a Moore matrix, introduced by E. H. Moore (1896), is a matrix defined over a finite field. When it is a square matrix its determinant is called a Moore determinant (this is unrelated to the Moore determinant of a quaternionic Hermitian matrix). The Moore matrix has successive powers of the Frobenius automorphism applied to the first column, so it is an m × n matrix
or
for all indices i and j. (Some authors use the transpose of the above matrix.)
The Moore determinant of a square Moore matrix (so m = n) can be expressed as:
where c runs over a complete set of direction vectors, made specific by having the last non-zero entry equal to 1, i.e.
In particular the Moore determinant vanishes if and only if the elements in the left hand column are linearly dependent over the finite field of order q. So it is analogous to the Wronskian of several functions.
Dickson used the Moore determinant in finding the modular invariants of the general linear group over a finite field.
See also
- Alternant matrix
- Vandermonde determinant
- List of matrices
References
- Dickson, Leonard Eugene (1958) [1901], Magnus, Wilhelm, ed., Linear groups: With an exposition of the Galois field theory, Dover Phoenix editions, New York: Dover Publications, ISBN 978-0-486-49548-4, MR 0104735
- David Goss (1996). Basic Structures of Function Field Arithmetic. Springer Verlag. ISBN 3-540-63541-6. Chapter 1.
- Moore, E. H. (1896), "A two-fold generalization of Fermat's theorem.", American M. S. Bull. 2: 189–199, doi:10.1090/S0002-9904-1896-00337-2, JFM 27.0139.05