Monk's formula
In mathematics, Monk's formula, found by Monk (1959), is an analogue of Pieri's formula that describes the product of a linear Schubert polynomial by a Schubert polynomial. Equivalently, it describes the product of a special Schubert cycle by a Schubert cycle in the cohomology of a flag manifold.
Write tij for the transposition (i j), and si = ti,i+1. Then 𝔖sr = x1 + ⋯ + xr, and Monk's formula states that for a permutation w,
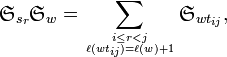
where  is the length of w. The pairs (i, j) appearing in the sum are exactly those such that i ≤ r < j, wi < wj, and there is no i < k < j with wi < wk < wj; each wtij is a cover of w in Bruhat order.
is the length of w. The pairs (i, j) appearing in the sum are exactly those such that i ≤ r < j, wi < wj, and there is no i < k < j with wi < wk < wj; each wtij is a cover of w in Bruhat order.