Modulus of smoothness
In mathematics, moduli of smoothness are used to quantitatively measure smoothness of functions. Moduli of smoothness generalise modulus of continuity and are used in approximation theory and numerical analysis to estimate errors of approximation by polynomials and splines.
Moduli of smoothness
The modulus of smoothness of order  [1]
of a function
[1]
of a function ![f\in C[a,b]](../I/m/f11b0f373b84297350cd9c1fa397c30b.png) is the function
is the function 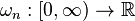 defined by
defined by
and
where we the finite difference (n-th order forward difference) are defined as
Properties
1. 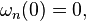
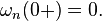
2. 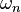 is non-decreasing on
is non-decreasing on 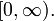
3. 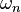 is continuous on
is continuous on 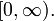
4. 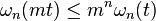 ,
, 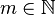 ,
, 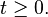
5. 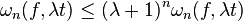 ,
, 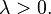
6. For 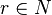 , denote by
, denote by 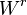 the space of continuous function on
the space of continuous function on ![[-1,1]](../I/m/d060b17b29e0dae91a1cac23ea62281a.png) that have
that have 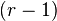 -st absolutely continuous derivative on
-st absolutely continuous derivative on ![[-1,1]](../I/m/d060b17b29e0dae91a1cac23ea62281a.png) and
and ![\|f^{(r)}\|_{L_{\infty}[-1,1]}<+\infty.](../I/m/d08c4d25797616f810a2d6e81f89c2f4.png) If
If 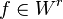 , then
, then ![\omega_r(t,f,[-1,1])\leq t^r\|f^{(r)}\|_{L_{\infty}[-1,1]}, t\geq 0,](../I/m/922dca09010799b298dfa98992b277a2.png) where
where ![\|g(x)\|_{L_{\infty}[-1,1]}={\mathrm{ess} \sup}_{x\in [-1,1]}|g(x)|.](../I/m/9850db75923a2f333019b5bcd305320c.png)
Applications
Moduli of smoothness can be used to prove estimates on the error of approximation. Due to property (6), moduli of smoothness provide more general estimates than the estimates in terms of derivatives.
For example, moduli of smoothness are used in Whitney inequality to estimate the error of local polynomial approximation. Another application is given by the following more general version of Jackson inequality:
For every natural number  , if
, if  is
is 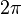 -periodic continuous function, there exists a trigonometric polynomial
-periodic continuous function, there exists a trigonometric polynomial 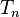 of degree
of degree 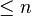 such that
such that
where the constant 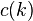 depends on
depends on 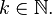
References
- ↑ DeVore, Ronald A., Lorentz, George G., Constructive approximation, Springer-Verlag, 1993.
![\omega_n(t,f,[a,b])=\sup_{h\in[0,t]}\sup_{x\in[a,b-nh]}|\Delta_h^n(f,x)|\text{ for }0\le t\le \frac{b-a} n,](../I/m/72a86acb86595948a96720d6d2c02e8f.png)
![\omega_n(t,f,[a,b])=\omega_n\left(\frac{b-a}{n},f,[a,b]\right),\text{ for }t>\frac{b-a}{n},](../I/m/a3eb412c0ff668c590e0149edc403fbb.png)
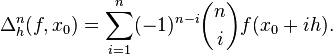
![|f(x)-T_n(x)|\leq c(k)\omega_k\left(\frac{1}{n},f\right),\quad x\in[0,2\pi],](../I/m/4a6fb481ab87a0cac61743befef4440e.png)