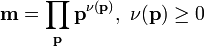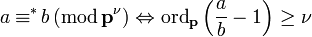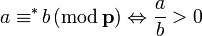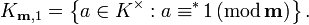Modulus (algebraic number theory)
In mathematics, in the field of algebraic number theory, a modulus (plural moduli) (or cycle,[1] or extended ideal[2]) is a formal product of places of a global field (i.e. an algebraic number field or a global function field). It is used to encode ramification data for abelian extensions of a global field.
Definition
Let K be a global field with ring of integers R. A modulus is a formal product[3][4]
where p runs over all places of K, finite or infinite, the exponents ν(p) are zero except for finitely many p. If K is a number field, ν(p) = 0 or 1 for real places and ν(p) = 0 for complex places. If K is a function field, ν(p) = 0 for all infinite places.
In the function field case, a modulus is the same thing as an effective divisor,[5] and in the number field case, a modulus can be considered as special form of Arakelov divisor.[6]
The notion of congruence can be extended to the setting of moduli. If a and b are elements of K×, the definition of a ≡∗b (mod pν) depends on what type of prime p is:[7][8]
- if it is finite, then
- where ordp is the normalized valuation associated to p;
- if it is a real place (of a number field) and ν = 1, then
- under the real embedding associated to p.
- if it is any other infinite place, there is no condition.
Then, given a modulus m, a ≡∗b (mod m) if a ≡∗b (mod pν(p)) for all p such that ν(p) > 0.
Ray class group
The ray modulo m is[9][10][11]
A modulus m can be split into two parts, mf and m∞, the product over the finite and infinite places, respectively. Let Im to be one of the following:
- if K is a number field, the subgroup of the group of fractional ideals generated by ideals coprime to mf;[12]
- if K is a function field of an algebraic curve over k, the group of divisors, rational over k, with support away from m.[13]
In both case, there is a group homomorphism i : Km,1 → Im obtained by sending a to the principal ideal (resp. divisor) (a).
The ray class group modulo m is the quotient Cm = Im / i(Km,1).[14][15] A coset of i(Km,1) is called a ray class modulo m.
Erich Hecke's original definition of Hecke characters may be interpreted in terms of characters of the ray class group with respect to some modulus m.[16]
Properties
When K is a number field, the following properties hold.[17]
- When m = 1, the ray class group is just the ideal class group.
- The ray class group is finite. Its order is the ray class number.
- The ray class number is divisible by the class number of K.
Notes
- ↑ Lang 1994, §VI.1
- ↑ Cohn 1985, definition 7.2.1
- ↑ Janusz 1996, §IV.1
- ↑ Serre 1988, §III.1
- ↑ Serre 1988, §III.1
- ↑ Neukirch 1999, §III.1
- ↑ Janusz 1996, §IV.1
- ↑ Serre 1988, §III.1
- ↑ Milne 2008, §V.1
- ↑ Janusz 1996, §IV.1
- ↑ Serre 1988, §VI.6
- ↑ Janusz 1996, §IV.1
- ↑ Serre 1988, §V.1
- ↑ Janusz 1996, §IV.1
- ↑ Serre 1988, §VI.6
- ↑ Neukirch 1999, §VII.6
- ↑ Janusz & 1996 §4.1
References
- Cohn, Harvey (1985), Introduction to the construction of class fields, Cambridge studies in advanced mathematics 6, Cambridge University Press, ISBN 978-0-521-24762-7
- Janusz, Gerald J. (1996), Algebraic number fields, Graduate Studies in Mathematics 7, American Mathematical Society, ISBN 978-0-8218-0429-2
- Lang, Serge (1994), Algebraic number theory, Graduate Texts in Mathematics 110 (2 ed.), New York: Springer-Verlag, ISBN 978-0-387-94225-4, MR 1282723
- Milne, James (2008), Class field theory (v4.0 ed.), retrieved 2010-02-22
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, Zbl 0956.11021, MR 1697859
- Serre, Jean-Pierre (1988), Algebraic groups and class fields, Graduate Texts in Mathematics 117, New York: Springer-Verlag, ISBN 978-0-387-96648-9