Moduli stack of formal group laws
In algebraic geometry, the moduli stack of formal group laws is a stack classifying formal group laws and isomorphisms between them. It is denoted by 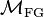 . It is a "geometric “object" that underlies the chromatic approach to the stable homotopy theory, a branch of algebraic topology.
. It is a "geometric “object" that underlies the chromatic approach to the stable homotopy theory, a branch of algebraic topology.
Currently, it is not known whether 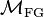 is a derived stack or not. Hence, it is typical to work with stratifications. Let
is a derived stack or not. Hence, it is typical to work with stratifications. Let 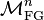 be given so that
be given so that 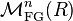 consists of formal group laws over R of height exactly n. They form a stratification of the moduli stack
consists of formal group laws over R of height exactly n. They form a stratification of the moduli stack 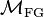 .
. 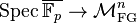 is faithfully flat. In fact,
is faithfully flat. In fact, 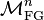 is of the form
is of the form 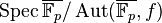 where
where 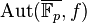 is a profinite group called the Morava stabilizer group. The Lubin–Tate theory describes how the strata
is a profinite group called the Morava stabilizer group. The Lubin–Tate theory describes how the strata 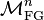 fit together.
fit together.
References
- J. Lurie, Chromatic Homotopy Theory (252x)
- P. Goerss, Realizing families of Landweber exact homology theories