Modal μ-calculus
In theoretical computer science, the modal μ-calculus (Lμ, Lμ, sometimes just μ-calculus, although this can have a more general meaning) is an extension of propositional modal logic (with many modalities) by adding a least fixpoint operator μ and a greatest fixpoint operator 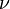 , thus a fixed-point logic.
, thus a fixed-point logic.
The (propositional, modal) μ-calculus originates with Dana Scott and Jaco de Bakker,[1] and was further developed by Dexter Kozen into the version most used nowadays. It is used to describe properties of labelled transition systems and for verifying these properties. Many temporal logics can be encoded in the μ-calculus, including CTL* and its widely used fragments—linear temporal logic and computational tree logic.[2]
An algebraic view is to see it as an algebra of monotonic functions over a complete lattice, with operators consisting of functional composition plus the least and greatest fixed point operators; from this viewpoint, the modal μ-calculus is over the lattice of a power set algebra.[3] The game semantics of μ-calculus is related to two-player games with perfect information, particularly infinite parity games.[4]
Syntax
Let P (propositions) and A (actions) be two finite sets of symbols, and let V be a countably infinite set of variables. The set of formulas of (propositional, modal) μ-calculus is defined as follows:
- each proposition and each variable is a formula;
- if
 and
and 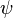 are formulas, then
are formulas, then 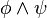 is a formula.
is a formula. - if
 is a formula, then
is a formula, then 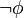 is a formula;
is a formula; - if
 is a formula and
is a formula and  is an action, then
is an action, then ![[a] \phi](../I/m/477c7497d86f850a1bd79a9ac5a97c1a.png) is a formula;(pronounced either:
is a formula;(pronounced either:  box
box  or after
or after  necessarily
necessarily  )
) - if
 is a formula and
is a formula and  a variable, then
a variable, then 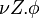 is a formula, provided that every free occurrence of
is a formula, provided that every free occurrence of  in
in  occurs positively, i.e. within the scope of an even number of negations.
occurs positively, i.e. within the scope of an even number of negations.
(The notions of free and bound variables are as usual, where 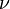 is the only binding operator.)
is the only binding operator.)
Given the above definitions, we can enrich the syntax with:
-
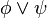 meaning
meaning 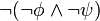
-
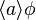 (pronounced either:
(pronounced either:  diamond
diamond  or after
or after  possibly
possibly  ) meaning
) meaning ![\neg [a] \neg \phi](../I/m/e75297fd7eb990948bef9f95e2f343f7.png)
-
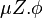 means
means ![\neg \nu Z. \neg \phi [Z:=\neg Z]](../I/m/d688e3c6cc6b71f9d56caeb072ec949d.png) , where
, where ![\phi [Z:=\neg Z]](../I/m/3ffc165e1929366a1acaa34a913aac67.png) means substituting
means substituting 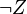 for Z in all free occurrences of Z in
for Z in all free occurrences of Z in  .
.
The first two formulas are the familiar ones from the classical propositional calculus and respectively the minimal multimodal logic K.
The notation 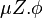 (and its dual) are inspired from the lambda calculus; the intent is to denote the least (and respectively greatest) fixed point of the expression
(and its dual) are inspired from the lambda calculus; the intent is to denote the least (and respectively greatest) fixed point of the expression  where the "minimization" (and respectively "maximization") are in the variable Z, much like in lambda calculus
where the "minimization" (and respectively "maximization") are in the variable Z, much like in lambda calculus 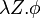 is a function with formula
is a function with formula  in bound variable Z;[5] see the denotational semantics below for details.
in bound variable Z;[5] see the denotational semantics below for details.
Denotational semantics
Models of (propositional) μ-calculus are given as labelled transition systems 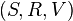 where:
where:
-
 is a set of states;
is a set of states; -
 maps to each label
maps to each label  a relation on
a relation on  ;
; -
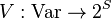 , maps to each proposition
, maps to each proposition 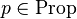 the set of states where the proposition is true.
the set of states where the proposition is true.
Given a labelled transition system 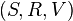 and an interpretation
and an interpretation  of the formulas
of the formulas  of
of  -calculus,
-calculus, ![[\![\underline{~\,}]\!]_i : \phi \rightarrow 2^S](../I/m/7c15b0e8895a3a207c04de4670029fd2.png) , is the function defined by the following rules:
, is the function defined by the following rules:
-
![[\![p]\!]_i = V(p)](../I/m/d5197bb1a64c2b039545562a446c0d0a.png) ;
; -
![[\![\phi \wedge \psi]\!]_i = [\![\phi]\!]_i \cap [\![\psi]\!]_i](../I/m/2585f2fc6f6a4a807c8c270d79612136.png) ;
; -
![[\![\neg \phi]\!]_i = S \smallsetminus [\![\phi]\!]_i](../I/m/8159d36c60581347528ef496b03efd7d.png) ;
; -
![[\![[a] \phi]\!]_i = \{s \in S \mid \forall t \in S, (s, t) \in R_a \rightarrow t \in [\![\phi]\!]_i\}](../I/m/966cfffd23632f94db6c3be4085469d1.png) ;
; -
![[\![\nu Z. \phi]\!]_i = \bigcup \{T \subseteq S \mid T \subseteq [\![\phi]\!]_{i[Z := T]}\}](../I/m/53b027e41c4cfefeccca13ff375cc4ee.png) , where
, where ![i[Z := T]](../I/m/0b6dcfa6a6ddc43521ceb7523bad38a2.png) maps Z to T while preserving the mappings of
maps Z to T while preserving the mappings of  everywhere else.
everywhere else.
By duality, the interpretation of the other basic formulas is:
-
![[\![\phi \vee \psi]\!]_i = [\![\phi]\!]_i \cup [\![\psi]\!]_i](../I/m/0d934644136f16e6ecbbb761fa0d387c.png) ;
; -
![[\![\langle a \rangle \phi]\!]_i = \{s \in S \mid \exists t \in S, (s, t) \in R_a \wedge t \in [\![\phi]\!]_i\}](../I/m/b1ae9ba3a322f64eccf5c9a3e9a275ca.png) ;
; -
![[\![\mu Z. \phi]\!]_i = \bigcap \{T \subseteq S \mid [\![\phi]\!]_{i[Z := T]} \subseteq T \}](../I/m/c449800e024a142cf11690ece4065660.png)
Less formally, this means that, for a given transition system 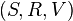 :
:
-
 holds in the set of states
holds in the set of states 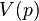 ;
; -
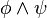 holds in every state where
holds in every state where  and
and 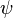 both hold;
both hold; -
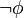 holds in every state where
holds in every state where  does not hold.
does not hold. -
![[a] \phi](../I/m/477c7497d86f850a1bd79a9ac5a97c1a.png) holds in a state
holds in a state  if every
if every  -transition leading out of
-transition leading out of  leads to a state where
leads to a state where  holds.
holds. -
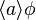 holds in a state
holds in a state  if there exists
if there exists  -transition leading out of
-transition leading out of  that leads to a state where
that leads to a state where  holds.
holds. -
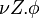 holds in any state in any set
holds in any state in any set  such that, when the variable
such that, when the variable  is set to
is set to  , then
, then  holds for all of
holds for all of  . (From the Knaster–Tarski theorem it follows that
. (From the Knaster–Tarski theorem it follows that ![[\![\nu Z.\phi]\!]_i](../I/m/34b9f655b0d2ab1aa9fcf19de1cd4715.png) is the greatest fixpoint of
is the greatest fixpoint of ![[\![\phi]\!]_{i[Z := T]}](../I/m/7ab456d6d5afe118e431dd836f51aa9e.png) , and
, and ![[\![\mu Z. \phi]\!]_i](../I/m/e39ac5598049acddcb06e7b100d9ff50.png) its least fixpoint.)
its least fixpoint.)
The interpretations of ![[a] \phi](../I/m/477c7497d86f850a1bd79a9ac5a97c1a.png) and
and 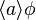 are if fact the "classical" ones from dynamic logic. Additionally, the operator μ can be interpreted as liveness ("something good eventually happens") and ν as safety ("nothing bad ever happens") in Leslie Lamport's informal classification.[6]
are if fact the "classical" ones from dynamic logic. Additionally, the operator μ can be interpreted as liveness ("something good eventually happens") and ν as safety ("nothing bad ever happens") in Leslie Lamport's informal classification.[6]
Examples
-
![\nu Z.\phi \wedge [a]Z](../I/m/02914e47be2a3a1357d398d3ea761c04.png) is interpreted as "
is interpreted as " is true along every a-path".[6]
is true along every a-path".[6] -
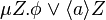 is interpreted as the existence of a path along a-transitions to a state where
is interpreted as the existence of a path along a-transitions to a state where  holds.[7]
holds.[7] - The property of a system of being deadlock-free, understood as having no states without outgoing transitions and furthermore there does not exists a path to such a state, is expressed by formula[7]
-
Satisfiability
Satisfiability of a modal μ-calculus formula is EXPTIME-complete.[8]
See also
- Finite model theory
- Alternation-free modal μ-calculus
Notes
- ↑ Kozen p. 333.
- ↑ Clarke p.108, Theorem 6; Emerson p. 196
- ↑ Arnold and Niwiński, pp. viii-x and chapter 6
- ↑ Arnold and Niwiński, pp. viii-x and chapter 4
- ↑ Arnold and Niwiński, p. 14
- ↑ 6.0 6.1 Bradfield and Stirling, p. 731
- ↑ 7.0 7.1 Erich Grädel; Phokion G. Kolaitis; Leonid Libkin; Maarten Marx, Joel Spencer, Moshe Y. Vardi, Yde Venema, Scott Weinstein (2007). Finite Model Theory and Its Applications. Springer. p. 159. ISBN 978-3-540-00428-8.
- ↑ Klaus Schneider (2004). Verification of reactive systems: formal methods and algorithms. Springer. p. 521. ISBN 978-3-540-00296-3.
References
- Clarke, Jr., Edmund M.; Orna Grumberg; Doron A. Peled (1999). Model Checking. Cambridge, Massachusetts, USA: MIT press. ISBN 0-262-03270-8., chapter 7, Model checking for the μ-calculus, pp. 97–108
- Stirling, Colin. (2001). Modal and Temporal Properties of Processes. New York, Berlin, Heidelberg: Springer Verlag. ISBN 0-387-98717-7., chapter 5, Modal μ-calculus, pp. 103–128
- André Arnold; Damian Niwiński (2001). Rudiments of μ-Calculus. Elsevier. ISBN 978-0-444-50620-7., chapter 6, The μ-calculus over powerset algebras, pp. 141–153 is about the modal μ-calculus
- Yde Venema (2008) Lectures on the Modal μ-calculus; was presented at The 18th European Summer School in Logic, Language and Information
- Bradfield, Julian and Stirling, Colin (2006). "Modal mu-calculi". In P. Blackburn, J. van Benthem and F. Wolter (eds.). The Handbook of Modal Logic. Elsevier. pp. 721–756.
- Emerson, E. Allen (1996). "Model Checking and the Mu-calculus". Descriptive Complexity and Finite Models. American Mathematical Society. pp. 185–214. ISBN 0-8218-0517-7.
- Kozen, Dexter (1983). "Results on the Propositional μ-Calculus". Theoretical Computer Science 27 (3): 333–354. doi:10.1016/0304-3975(82)90125-6.
External links
- Sophie Pinchinat, Logic, Automata & Games video recording of a lecture at ANU Logic Summer School '09
![\nu Z.(\bigvee_{a\in A}\langle a\rangle\top\wedge \bigwedge_{a\in A}[a]Z)](../I/m/21f69b1713d64ebfc1b658df153a8383.png)