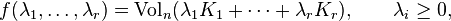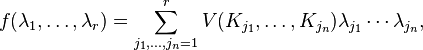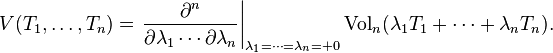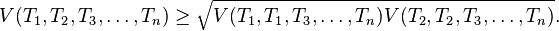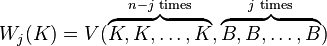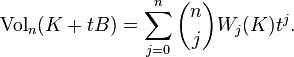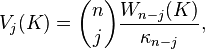Mixed volume
In mathematics, more specifically, in convex geometry, the mixed volume is a way to associate a non-negative number to an n-tuple of convex bodies in the n-dimensional space. This number depends on the size of the bodies and their relative positions.[1]
Definition
Let K1, K2, ..., Kr be convex bodies in Rn, and consider the function
where Voln stands for the n-dimensional volume and its argument is the Minkowski sum of the scaled convex bodies Ki. One can show that f is a homogeneous polynomial of degree n, therefore it can be written as
where the functions V are symmetric. Then V(T1, ..., Tn) is called the mixed volume of T1, T2, ..., Tn.
Equivalently,
Properties
- The mixed volume is uniquely determined by the following three properties:
- V(T, ...., T) = Voln(T);
- V is symmetric in its arguments;
- V is multilinear: V(a T + b S, T2, ..., Tn) =a V(T, T2, ..., Tn) + b V(S, T2, ..., Tn) for a,b ≥ 0.
- The mixed volume is non-negative, and increasing in each variable.
- The Alexandrov–Fenchel inequality, discovered by Aleksandr Danilovich Aleksandrov and Werner Fenchel:
- Numerous geometric inequalities, such as the Brunn–Minkowski inequality for convex bodies and Minkowski's first inequality, are special cases of the Alexandrov–Fenchel inequality.
Quermassintegrals
Let K ⊂ Rn be a convex body, and let B ⊂ Rn be the Euclidean ball. The mixed volume
is called the j-th quermassintegral of K.[2]
The definition of mixed volume yields the Steiner formula (named after Jakob Steiner):
Intrinsic volumes
The j-th intrinsic volume of K is defined by
where κn−j is the volume of the (n − j)-dimensional ball.
Hadwiger's characterization theorem
Hadwiger's theorem asserts that every valuation on convex bodies in Rn that is continuous and invariant under rigid motions of Rn is a linear combination of the quermassintegrals (or, equivalently, of the intrinsic volumes).[3]
Notes
- ↑ Burago, Yu.D. (2001), "Mixed volume theory", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- ↑ McMullen, P. (1991). "Inequalities between intrinsic volumes". Monatsh. Math. 111 (1): 47–53. doi:10.1007/bf01299276. MR 1089383.
- ↑ Klain, D.A. (1995). "A short proof of Hadwiger's characterization theorem". Mathematika 42 (2): 329–339. doi:10.1112/s0025579300014625. MR 1376731.