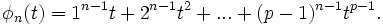Mirimanoff's congruence

In number theory, a branch of mathematics, a Mirimanoff's congruence is one of a collection of expressions in modular arithmetic which, if they hold, entail the truth of Fermat's Last Theorem. Since the theorem has now been proven, these are now of mainly historical significance, though the Mirimanoff polynomials are interesting in their own right. The theorem is due to Dmitry Mirimanoff.

Definition

The nth Mirimanoff polynomial for the prime p is

\phi_n(t) = 1^{n-1}t + 2^{n-1}t^2 + ... + (p-1)^{n-1} t^{p-1}.

In terms of these polynomials, if t is one of the six values {-X/Y, -Y/X, -X/Z, -Z/X, -Y/Z, -Z/Y} where X^p+Y^p+Z^p=0 is a solution to Fermat's Last Theorem, then

φ_p-1(t) ≡ 0 (mod p)
φ_p-2(t)φ₂(t) ≡ 0 (mod p)
φ_p-3(t)φ₃(t) ≡ 0 (mod p)

...

φ_(p+1)/2(t)φ_(p-1)/2(t) ≡ 0 (mod p)

Other congruences

Mirimanoff also proved the following:

If an odd prime p does not divide one of the numerators of the Bernoulli numbers B_p-3, B_p-5, B_p-7 or B_p-9, then the first case of Fermat's Last Theorem, where p does not divide X, Y or Z in the equation X^p+Y^p+Z^p=0, holds.

If the first case of Fermat's Last Theorem fails for the prime p, then 3^p-1 ≡ 1 (mod p²). A prime number with this property is sometimes called a Mirimanoff prime, in analogy to a Wieferich prime which is a prime such that 2^p-1 ≡ 1 (mod p²). The existence of primes satisfying such congruences was recognized long before their implications for the first case of Fermat's Last Theorem became apparent; but while the discovery of the first Wieferich prime came after these theoretical developments and was prompted by them, the first instance of a Mirimanoff prime is so small that it was already known before Mirimanoff formulated the connection to FLT in 1910, which fact may explain the reluctance of some writers to use the name. So early as his 1895 paper (p. 298), Mirimanoff alludes to a rather complicated test for the primes now known by his name, deriving from a formula published by Sylvester in 1861, which is of little computational value but great theoretical interest. This test was considerably simplified by Lerch (1905), p. 476, who showed that in general, for p > 3,

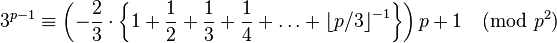
$3^{p-1} \equiv \left(- \frac 23 \cdot \left\{ 1 + \frac 12 + \frac 13 + \frac 14 + \ldots + \left\lfloor p/3 \right\rfloor^{-1}\right\}\right)p + 1 \pmod {p^2}$

so that a prime possesses the Mirimanoff property if it divides the expression within the curly braces. The condition was further refined in an important paper by Emma Lehmer (1938), in which she considered the intriguing and still unanswered question of whether it is possible for a number to satisfy the congruences of Wieferich and Mirimanoff simultaneously. To date, the only known Mirimanoff primes are 11 and 1006003 (sequence A014127 in OEIS). The discovery of the second of these appears to be due to K.E. Kloss (1965).

References

K.E. Kloss, "Some Number-Theoretic Calculations," Journal of Research of the National Bureau of Standards—B. Mathematics and Mathematical Physics 69 (1965), pp. 335–336.
Emma Lehmer, "On Congruences involving Bernoulli Numbers and the Quotients of Fermat and Wilson," Annals of Mathematics 39 (1938), pp. 350–360.
M. Lerch, "Zur Theorie des Fermatschen Quotienten…," Mathematische Annalen 60 (1905), pp. 471–490 .
D. Mirimanoff, "Sur la Congruence (r^p−1 − 1):p ≡ q_r," Journal für die reine und angewandte Mathematik 115 (1895), pp. 295–300 . Some corrections are given in the 1937 paper below.
D. Mirimanoff, "Sur le dernier théorème de Fermat et le Critérium de M. A. Wieferich," L'Enseignement Mathématique 11 (1909), pp. 455–459 .
D. Mirimanoff, "Sur le dernier théorème de Fermat," Comptes rendus hebdomadaires des séances de l'Académie des Sciences 150 (1910), pp. 204–206; a revised and expanded version of this paper appeared under the same title in Journal für die reine und angewandte Mathematik 139 (1911), pp. 309–324 .
D. Mirimanoff, "Sur les nombres de Bernoulli," L'Enseignement Mathématique 36 (1937), pp. 228–235 .
Paulo Ribenboim, 13 Lectures on Fermat's Last Theorem, Springer, 1979
Paulo Ribenboim, My Numbers, My Friends: Popular Lectures on Number Theory, Springer, 2006