Minimum message length

Minimum message length (MML) is a formal information theory restatement of Occam's Razor: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct (where the message consists of a statement of the model, followed by a statement of data encoded concisely using that model). MML was invented by Chris Wallace, first appearing in the seminal (Wallace and Boulton, 1968).

MML is intended not just as a theoretical construct, but as a technique that may be deployed in practice. It differs from the related concept of Kolmogorov complexity in that it does not require use of a Turing-complete language to model data. The relation between Strict MML (SMML) and Kolmogorov complexity is outlined in Wallace and Dowe (1999a). Further, a variety of mathematical approximations to "Strict" MML can be used — see, e.g., Chapters 4 and 5 of Wallace (posthumous) 2005.

Definition

Shannon's A Mathematical Theory of Communication (1949) states that in an optimal code, the message length (in binary) of an event , , where has probability 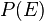, is given by .

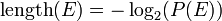Bayes's theorem states that the probability of a (variable) hypothesis given fixed evidence is proportional to 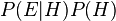, which, by the definition of conditional probability, is equal to 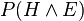. We want the model (hypothesis) with the highest such posterior probability. Suppose we encode a message which represents (describes) both model and data jointly. Since 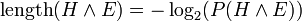, the most probable model will have the shortest such message. The message breaks into two parts: 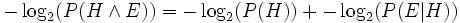. The first part encodes the model itself. The second part contains information (e.g., values of parameters, or initial conditions, etc.) that, when processed by the model, outputs the observed data.

MML naturally and precisely trades model complexity for goodness of fit. A more complicated model takes longer to state (longer first part) but probably fits the data better (shorter second part). So, an MML metric won't choose a complicated model unless that model pays for itself.

Continuous-valued parameters

One reason why a model might be longer would be simply because its various parameters are stated to greater precision, thus requiring transmission of more digits. Much of the power of MML derives from its handling of how accurately to state parameters in a model, and a variety of approximations that make this feasible in practice. This allows it to usefully compare, say, a model with many parameters imprecisely stated against a model with fewer parameters more accurately stated.

Key features of MML

• MML can be used to compare models of different structure. For example, its earliest application was in finding mixture models with the optimal number of classes. Adding extra classes to a mixture model will always allow the data to be fitted to greater accuracy, but according to MML this must be weighed against the extra bits required to encode the parameters defining those classes.
• MML is a method of Bayesian model comparison. It gives every model a score.
• MML is scale-invariant and statistically invariant. Unlike many Bayesian selection methods, MML doesn't care if you change from measuring length to volume or from Cartesian co-ordinates to polar co-ordinates.
• MML is statistically consistent. For problems like the Neyman-Scott (1948) problem or factor analysis where the amount of data per parameter is bounded above, MML can estimate all parameters with statistical consistency.
• MML accounts for the precision of measurement. It uses the Fisher information (in the Wallace-Freeman 1987 approximation, or other hyper-volumes in other approximations) to optimally discretize continuous parameters. Therefore the posterior is always a probability, not a probability density.
• MML has been in use since 1968. MML coding schemes have been developed for several distributions, and many kinds of machine learners including unsupervised classification, decision trees and graphs, DNA sequences, Bayesian networks, neural networks (one-layer only so far), image compression, image and function segmentation, etc.

See also

• Algorithmic probability
• Algorithmic information theory
• Grammar induction
• Inductive inference
• Inductive probability
• Kolmogorov complexity — absolute complexity (within a constant, depending on the particular choice of Universal Turing Machine); MML is typically a computable approximation (see
• Minimum description length — a supposedly non-Bayesian alternative with a possibly different motivation, which was introduced 10 years later — for comparisons, see, e.g., (sec. 10.2 of Wallace (posthumous) 2005) and (sec. 11.4.3, pp 272-273 of Comley and Dowe, 2005) and the special issue on Kolmogorov Complexity in the Computer Journal: Vol. 42, No. 4, 1999.
• Occam's razor

Wallace and Dowe (1999a) below for elaboration)

External links

• Links to all Chris Wallace's known publications.
• C.S. Wallace, Statistical and Inductive Inference by Minimum Message Length, Springer-Verlag (Information Science and Statistics), ISBN 0-387-23795-X, May 2005 - chapter headings, table of contents and sample pages.
• A searchable database of Chris Wallace's publications.
• Minimum Message Length and Kolmogorov Complexity (by C.S. Wallace and D.L. Dowe, Computer Journal, Vol. 42, No. 4, 1999, pp270-283).
• History of MML, CSW's last talk.
• Message Length as an Effective Ockham's Razor in Decision Tree Induction, by S. Needham and D. Dowe, Proc. 8th International Workshop on AI and Statistics (2001), pp253-260. (Shows how Occam's razor works fine when interpreted as MML.)
• L.Allison,
• Models for machine learning and data mining in functional programming, J. Functional Programming, 15(1), pp15–32, Jan. 2005 (MML, FP, and Haskell code).
• J.W.Comley and D.L. Dowe (2005), "Minimum Message Length, MDL and Generalised Bayesian Networks with Asymmetric Languages", Chapter 11 (pp 265-294) in P. Grunwald, M. A. Pitt and I. J. Myung (ed.), Advances in Minimum Description Length: Theory and Applications, M.I.T. Press (MIT Press), April 2005, ISBN 0-262-07262-9.

[See also Comley and Dowe (2003), .pdf. Comley & Dowe (2003, 2005) are the first two papers on MML Bayesian nets using both discrete and continuous valued parameters.]

• Dowe, David L. (2010). MML, hybrid Bayesian network graphical models, statistical consistency, invariance and uniqueness, in Handbook of Philosophy of Science (Volume 7: Handbook of Philosophy of Statistics), Elsevier, ISBN 978-0-444-51862-0, pp 901-982.
• Minimum Message Length (MML), LA's MML introduction, (MML alt.).
• Minimum Message Length (MML), researchers and links.
• Another MML research website.
• Snob page for MML mixture modelling.
• MITECS: Chris Wallace wrote an entry on MML for MITECS. (Requires account)
• mikko.ps: Short introductory slides by Mikko Koivisto in Helsinki]
• Akaike information criterion (AIC) method of model selection, and a comparison with MML: D.L. Dowe, S. Gardner & G. Oppy (2007), "Bayes not Bust! Why Simplicity is no Problem for Bayesians", Brit. J. Philos. Sci., Vol. 58, Dec. 2007, pp709–754.