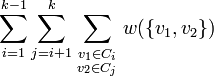Minimum k-cut
In mathematics, the minimum k-cut, is a combinatorial optimization problem that requires finding a set of edges whose removal would partition the graph to k connected components. These edges are referred to as k-cut. The goal is to find the minimum-weight k-cut. This partitioning can have applications in VLSI design, data-mining, finite elements and communication in parallel computing.
Formal definition
Given an undirected graph G = (V, E) with an assignment of weights to the edges w: E → N and an integer k ∈ {2, 3, …, |V|}, partition V into k disjoint sets F = {C1, C2, …, Ck} while minimizing
For a fixed k, the problem is polynomial time solvable in O(|V|k2).[1] However, the problem is NP-complete if k is part of the input.[2] It is also NP-complete if we specify  vertices and ask for the minimum
vertices and ask for the minimum  -cut which separates these vertices among each of the sets.[3]
-cut which separates these vertices among each of the sets.[3]
Approximations
Several approximation algorithms exist with an approximation of 2 − 2/k. A simple greedy algorithm that achieves this approximation factor computes a minimum cut in each connected components and removes the lightest one. This algorithm requires a total of n − 1 max flow computations. Another algorithm achieving the same guarantee uses the Gomory–Hu tree representation of minimum cuts. Constructing the Gomory–Hu tree requires n − 1 max flow computations, but the algorithm requires an overall O(kn) max flow computations. Yet, it is easier to analyze the approximation factor of the second algorithm.[4][5]
If we restrict the graph to a metric space, meaning a complete graph that satisfies the triangle inequality, and enforce that the output partitions are each of pre-specified sizes, the problem is approximable to within a factor of 3 for any fixed k.[6] More recently, polynomial time approximation schemes (PTAS) were discovered for those problems.[7]
See also
Notes
- ↑ Goldschmidt & Hochbaum 1988.
- ↑ Garey & Johnson 1979
- ↑ , which cites
- ↑ Saran & Vazirani 1991.
- ↑ Vazirani 2003, pp. 40–44.
- ↑ Guttmann-Beck & Hassin 1999, pp. 198–207.
- ↑ Fernandez de la Vega, Karpinski & Kenyon 2004
References
- Goldschmidt, O.; Hochbaum, D. S. (1988), Proc. 29th Ann. IEEE Symp. on Foundations of Comput. Sci., IEEE Computer Society, pp. 444–451
- Garey, M. R.; Johnson, D. S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 0-7167-1044-7
- Saran, H.; Vazirani, V. (1991), "Finding k-cuts within twice the optimal", Proc. 32nd Ann. IEEE Symp. on Foundations of Comput. Sci, IEEE Computer Society, pp. 743–751
- Vazirani, Vijay V. (2003), Approximation Algorithms, Berlin: Springer, ISBN 3-540-65367-8
- Guttmann-Beck, N.; Hassin, R. (1999), "Approximation algorithms for minimum k-cut", Algorithmica, pp. 198–207
- Comellas, Francesc; Sapena, Emili (2006), "A multiagent algorithm for graph partitioning. Lecture Notes in Comput. Sci.", Algorithmica 3907 (2): 279–285, doi:10.1007/s004530010013, ISSN 0302-9743
- Crescenzi, Pierluigi; Kann, Viggo; Halldórsson, Magnús; Karpinski, Marek; Woeginger, Gerhard (2000), "Minimum k-cut", A Compendium of NP Optimization Problems
- Fernandez de la Vega, W.; Karpinski, M.; Kenyon, C. (2004). "Approximation schemes for Metric Bisection and partitioning". Proceedings of the fifteenth annual ACM-SIAM symposium on Discrete Algorithms. pp. 506–515,.