Mingarelli identity

In the field of ordinary differential equations, the Mingarelli identity (coined by Philip Hartman[1]) is a theorem that provides criteria for the oscillation and non-oscillation of solutions of some linear differential equations in the real domain. It extends the Picone identity from two to three or more differential equations of the second order. Its most basic form appears here.

The identity

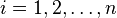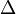Consider the n solutions of the following (uncoupled) system of second order linear differential equations over the t-interval [a, b]. (p_i(t) x_i^\prime)^\prime + q_i(t) x_i = 0, \,\,\,\,\,\,\,\,\,\, x_i(a)=1,\,\, x_i^\prime(a)=R_i\, where i=1,2, \ldots, n. Let \Delta denote the forward difference operator, i.e., 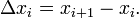\Delta x_i = x_{i+1}-x_i. The second order difference operator is found by iterating the first order operator as in 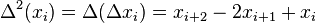\Delta^2 (x_i) = \Delta(\Delta x_i) = x_{i+2}-2x_{i+1}+x_{i}, with a similar definition for the higher iterates.

Leaving out the independent variable t for convenience, and assuming the 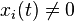x_i(t) \ne 0 on (a, b], there holds the identity,[2]

\begin{align} x_{n-1}^2\Delta^{n-1}(p_1r_1)]_a^b & = \int_a^b (x^\prime_{n-1})^2 \Delta^{n-1}(p_1) - \int_a^b x_{n-1}^2 \Delta^{n-1}(q_1) - \sum_{k=0}^{n-1} C(n-1,k)(-1)^{n-k-1}\int_a^b p_{k+1} W^2(x_{k+1},x_{n-1})/x_{k+1}^2, \end{align}

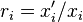where r_i = x^\prime_i/x_i is a logarithmic derivative, 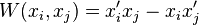W(x_i, x_j) = x^\prime_ix_j - x_ix^\prime_j, is a Wronskian and the 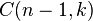C(n-1,k) are binomial coefficients. When 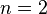n=2 this reduces to the Picone identity.

The above identity leads quickly to the following comparison theorem for three linear differential equations,[2] extending the Sturm–Picone comparison theorem.

Let 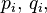p_i,\, q_i,\, i = 1, 2, 3 be real-valued continuous functions on the interval [a, b] and let

  1. (p_1(t) x_1^\prime)^\prime + q_1(t) x_1 = 0, \,\,\,\,\,\,\,\,\,\, x_1(a)=1,\,\, x_1^\prime(a)=R_1\,
  2. (p_2(t) x_2^\prime)^\prime + q_2(t) x_2 = 0, \,\,\,\,\,\,\,\,\,\, x_2(a)=1,\,\, x_2^\prime(a)=R_2\,
  3. (p_3(t) x_3^\prime)^\prime + q_3(t) x_3 = 0, \,\,\,\,\,\,\,\,\,\, x_3(a)=1,\,\, x_3^\prime(a)=R_3\,

be three homogeneous linear second order differential equations in self-adjoint form with

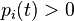p_i(t)>0\, for each i and for all t in [a, b], and where the 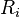R_i are arbitrary real numbers.

Assume that for all t in [a, b] we have,

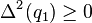\Delta^2(q_1) \ge 0 ,
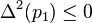\Delta^2(p_1) \le 0 ,
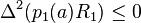\Delta^2(p_1(a)R_1) \le 0 .

If 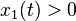x_1(t) > 0 on [a, b], and 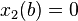x_2(b)=0, then any solution 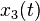x_3(t) has at least one zero in [a, b].

References

  1. ↑ Clark D.N., G. Pecelli, and R. Sacksteder 1981
  2. ↑ 2.0 2.1 Mingarelli 1979, p. 223