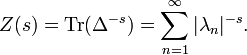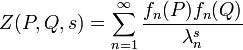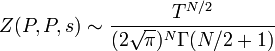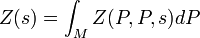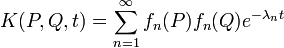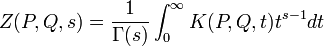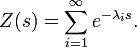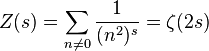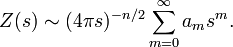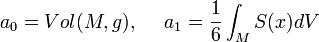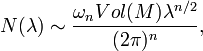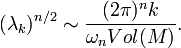Minakshisundaram–Pleijel zeta function
The Minakshisundaram–Pleijel zeta function is a zeta function encoding the eigenvalues of the Laplacian of a compact Riemannian manifold. It was introduced by Subbaramiah Minakshisundaram and Åke Pleijel (1949). The case of a compact region of the plane was treated earlier by Carleman (1935).
Definition
For a compact Riemannian manifold M of dimension N with eigenvalues
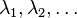 of the Laplace–Beltrami operator Δ the zeta function
is given for
of the Laplace–Beltrami operator Δ the zeta function
is given for 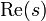 sufficiently large by
sufficiently large by
(where if an eigenvalue is zero it is omitted in the sum). The manifold may have a boundary, in which case one has to prescribe suitable boundary conditions, such as Dirichlet or Neumann boundary conditions.
More generally one can define
for P and Q on the manifold, where the fn are normalized eigenfunctions. This can be analytically continued to a meromorphic function of s for all complex s, and is holomorphic for P≠Q.
The only possible poles are simple poles at the points s = N/2, N/2−1, N/2−2,..., 1/2,−1/2, −3/2,... for N odd, and at the points s = N/2, N/2−1, N/2−2, ...,2, 1 for N even. If N is odd then Z(P,P,s) vanishes at s = 0, −1, −2,... If N is even its values can be explicitly by Wiener-Ikehara theorem as a corollary the relation
where the sign ~ indicates that the quotient of both the sides tend to 1 when T tends to +∞.
The function Z(s) can be recovered from this by integrating Z(P, P, s) over the whole manifold M:
Heat kernel
The analytic continuation of the zeta function can be found by expressing it in terms of the heat kernel
as the Mellin transform
In case of heat kernel, for given a Riemannian manifold (M,g) we can take the orthonormal basis of eigenfunctions and obtain the partition function
The poles of the zeta function can be found from the asymptotic behavior of the heat kernel as t→0.
Example
If the manifold is a circle of dimension N=1, then the eigenvalues of the Laplacian are n2 for integers n. The zeta function
where ζ is the Riemann zeta function.
Applications
Apply the method of heat kernel to asymptotic expansion for Riemannian manifold (M,g) we obtain the two following theorems. Both are the resolutions of the inverse problem in which we get the geometric properties or quantities from spectra of the operators.
1,Minakshisundaram-Pleijel Asymptotic Expansion
Let (M,g) be an n-dimensional Riemannian manifold. The following asymptotic expansions hold as t→0+:
In dim=2, this means that the integral of scalar curvature tells us the Euler characteristic of M, i.e. Gauss-Bonnet Theorem.
In particular,
where S(x) is scalar curvature, the trace of the Ricci curvature, on M.
2,Weyl Asymptotic Formula
Let M be a compact Riemannian manifold, with eigenvalues
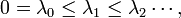 with each distinct eigenvalue repeated with its multiplicity. Define N(λ) to be the number of eigen values less than or equal to
with each distinct eigenvalue repeated with its multiplicity. Define N(λ) to be the number of eigen values less than or equal to  , and let
, and let 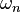 denote the volume of the unit disk in
denote the volume of the unit disk in 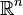 . Then
. Then
as λ→∞. Additionally, as k→∞,
This is also called Weyl's law, refined from Minakshisundaram-Pleijel asymptotic expansion.
References
- Berger, Marcel; Gauduchon, Paul; Mazet, Edmond (1971), Le spectre d'une variété riemannienne, Lecture Notes in Mathematics 194, Berlin, New York: Springer-Verlag, doi:10.1007/BFb0064643, MR 0282313
- Carleman, Torsten (1935), "Propriétés asymptotiques des fonctions fondamentales des membranes vibrantes.", 8. Skand. Mat.-Kongr. (in French): 34–44, Zbl 0012.07001
- Minakshisundaram, S.; Pleijel, Å. (1949), "Some properties of the eigenfunctions of the Laplace-operator on Riemannian manifolds", Canadian Journal of Mathematics 1: 242–256, doi:10.4153/CJM-1949-021-5, ISSN 0008-414X, MR 0031145