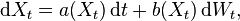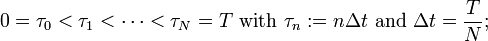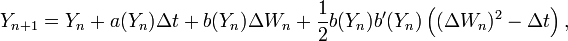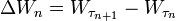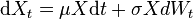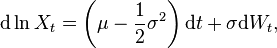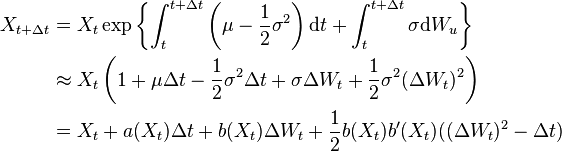Milstein method
In mathematics, the Milstein method is a technique for the approximate numerical solution of a stochastic differential equation. It is named after Grigori N. Milstein who first published the method in 1974.[1][2]
Description
Consider the autonomous Itō stochastic differential equation
with initial condition X0 = x0, where Wt stands for the Wiener process, and suppose that we wish to solve this SDE on some interval of time [0, T]. Then the Milstein approximation to the true solution X is the Markov chain Y defined as follows:
- partition the interval [0, T] into N equal subintervals of width
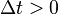 :
:
- set
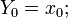
- recursively define
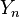 for
for 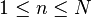 by
by
where 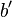 denotes the derivative of
denotes the derivative of 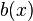 with respect to
with respect to  and
and
are independent and identically distributed normal random variables with expected value zero and variance 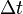 . Then
. Then 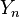 will approximate
will approximate 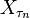 for
for 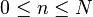 , and increasing
, and increasing  will yield a better approximation.
will yield a better approximation.
The error of the Milstein method is of order 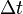 , which is considerably better than the Euler–Maruyama method, whose error is of order
, which is considerably better than the Euler–Maruyama method, whose error is of order 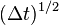 .[3]
.[3]
Intuitive derivation
For this derivation, we will only look at geometric Brownian motion (GBM), the stochastic differential equation of which is given by
with real constants  and
and  . Using Itō's lemma we get
. Using Itō's lemma we get
Thus, the solution to the GBM SDE is
where
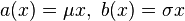 .
.
See also
References
- ↑ Mil'shtein, G. N. (1974). "Approximate integration of stochastic differential equations". Teor. Veroyatnost. i Primenen (in Russian) 19 (3): 583–588.
- ↑ Mil’shtejn, G. N. (1975). "Approximate Integration of Stochastic Differential Equations". Theory of Probability & Its Applications 19 (3): 557–000. doi:10.1137/1119062.
- ↑ V. Mackevičius, Introduction to Stochastic Analysis, Wiley 2011
Further reading
- Kloeden, P.E., & Platen, E. (1999). Numerical Solution of Stochastic Differential Equations. Springer, Berlin. ISBN 3-540-54062-8.