Milnor ring
In the mathematical discipline known as K-theory, the Milnor ring of a field F, named after John Milnor, is a graded ring 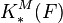 with unit, defined from F.
It has a generator
with unit, defined from F.
It has a generator 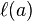 for each nonzero element a of the field, and is defined from these generators by the relations[1]
for each nonzero element a of the field, and is defined from these generators by the relations[1]
One can show that 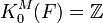 ,
, 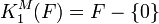 .
.
The Milnor ring appears on one side of the Milnor conjecture and the norm residue isomorphism theorem, which relate the Milnor ring to the Galois cohomology (or étale cohomology) of F.
References
- ↑ T.A. Springer, A remark on the Milnor ring, Inventiones mathematicae, 1970