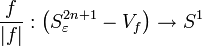Milnor map
In mathematics, Milnor maps are named in honor of John Milnor, who introduced them to topology and algebraic geometry in his book Singular Points of Complex Hypersurfaces (Princeton University Press, 1968) and earlier lectures. The most studied Milnor maps are actually fibrations, and the phrase Milnor fibration is more commonly encountered in the mathematical literature. The general definition is as follows.
Let 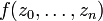 be a non-constant polynomial function of
be a non-constant polynomial function of 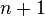 complex variables
complex variables 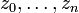 such that
such that 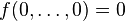 , so that the set
, so that the set 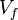 of all complex
of all complex 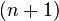 -vectors
-vectors 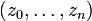 with
with 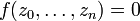 is a complex hypersurface of complex dimension
is a complex hypersurface of complex dimension  containing the origin of complex
containing the origin of complex 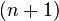 -space. (For instance, if
-space. (For instance, if 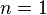 then
then 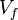 is a complex plane curve containing
is a complex plane curve containing 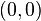 .) The argument of
.) The argument of  is the function
is the function
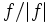 mapping the complement of
mapping the complement of 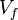 in complex
in complex 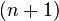 -space to the unit circle
-space to the unit circle 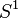 in C. For any real radius
in C. For any real radius 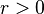 , the restriction of the argument of
, the restriction of the argument of  to the complement of
to the complement of 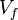 in the real
in the real 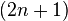 -sphere with center at the origin and radius
-sphere with center at the origin and radius  is the Milnor map of
is the Milnor map of  at radius
at radius  .
.
Milnor's Fibration Theorem states that, for every  such that the origin is a singular point of the hypersurface
such that the origin is a singular point of the hypersurface 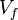 (in particular, for every non-constant square-free polynomial
(in particular, for every non-constant square-free polynomial  of two variables, the case of plane curves), then for
of two variables, the case of plane curves), then for  sufficiently small,
sufficiently small,
is a fibration. Each fiber is a non-compact differentiable manifold of real dimension 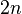 . Note that the closure of each fiber is a compact manifold with boundary. Here the boundary corresponds to the intersection of
. Note that the closure of each fiber is a compact manifold with boundary. Here the boundary corresponds to the intersection of 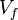 with the
with the 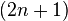 -sphere (of sufficiently small radius) and therefore it is a real manifold of dimension
-sphere (of sufficiently small radius) and therefore it is a real manifold of dimension 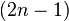 . Furthermore, this compact manifold with boundary, which is known as the Milnor fiber (of the isolated singular point of
. Furthermore, this compact manifold with boundary, which is known as the Milnor fiber (of the isolated singular point of  at the origin), is diffeomorphic to the intersection of the closed
at the origin), is diffeomorphic to the intersection of the closed 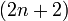 -ball (bounded by the small
-ball (bounded by the small 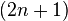 -sphere) with the (non-singular) hypersurface
-sphere) with the (non-singular) hypersurface 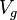 where
where 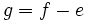 and
and  is any sufficiently small non-zero complex number. This small piece of hypersurface is also called a Milnor fiber.
is any sufficiently small non-zero complex number. This small piece of hypersurface is also called a Milnor fiber.
Milnor maps at other radii are not always fibrations, but they still have many interesting properties. For most (but not all) polynomials, the Milnor map at infinity (that is, at any sufficiently large radius) is again a fibration.
The Milnor map of 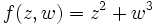 at any radius is a fibration; this construction gives the trefoil knot its structure as a fibered knot.
at any radius is a fibration; this construction gives the trefoil knot its structure as a fibered knot.
References
- Milnor, John W. (1968), Singular points of complex hypersurfaces, Annals of Mathematics Studies, No. 61. Princeton University Press, Princeton, NJ; University of Tokyo Press, Tokyo, ISBN 0-691-08065-8