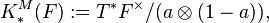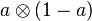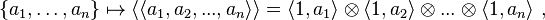Milnor K-theory

In mathematics, Milnor K-theory was an early attempt to define higher algebraic K-theory, introduced by Milnor (1970).

Definition

The calculation of K₂ of a field F led Milnor to the following ad hoc definition of "higher" K-groups by

K^M_*(F) := T^*F^\times/(a\otimes (1-a)), \,

thus as graded parts of a quotient of the tensor algebra of the multiplicative group F^× by the two-sided ideal, generated by the

a\otimes(1-a) \,

for a ≠ 0, 1. For n = 0,1,2 these coincide with Quillen's K-groups of a field, but for n ≧ 3 they differ in general. We define the symbol 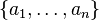$\{a_1,\ldots,a_n\}$ as the image of 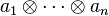$a_1 \otimes \cdots \otimes a_n$ : the case n=2 is a Steinberg symbol.^[1]

The tensor product on the tensor algebra induces a product 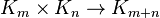$K_m \times K_n \rightarrow K_{m+n}$ making 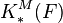$K^M_*(F)$ a graded ring which is graded-commutative.^[2]

Examples

For example, we have 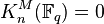$K^M_n(\mathbb{F}_q) = 0$ for n ≧ 2; 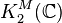$K^M_2(\mathbb{C})$ is an uncountable uniquely divisible group; 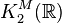$K^M_2(\mathbb{R})$ is the direct sum of a cyclic group of order 2 and an uncountable uniquely divisible group; 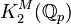$K^M_2(\mathbb{Q}_p)$ is the direct sum of the multiplicative group of $\mathbb{F}_p$ and an uncountable uniquely divisible group; 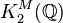$K^M_2(\mathbb{Q})$ is the direct sum of the cyclic group of order 2 and cyclic groups of order 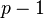$p-1$ for all odd prime $p$ .

Applications

Milnor K-theory plays a fundamental role in higher class field theory, replacing 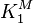$K^M_1$ in the one-dimensional class field theory.

Milnor K-theory modulo 2, denoted k_*(F) is related to étale (or Galois) cohomology of the field F by the Milnor conjecture, proven by Voevodsky. The analogous statement for odd primes is the Bloch–Kato conjecture, proved by Voevodsky, Rost, and others.

There are homomorphisms from k_n(F) to the Witt ring of F by taking the symbol

\{a_1,\ldots,a_n\} \mapsto \langle \langle a_1, a_2, ... , a_n \rangle \rangle = \langle 1, a_1 \rangle \otimes \langle 1, a_2 \rangle \otimes ... \otimes \langle 1, a_n \rangle \ ,

where the image is a Pfister form of dimension 2ⁿ.^[1] The image can be taken as Iⁿ/Iⁿ⁺¹ and the map is surjective since the Pfister forms additively generate Iⁿ.^[3] The Milnor conjecture can be interpreted as stating that these maps are isomorphisms.^[1]

References

↑ 1.0 1.1 1.2 Lam (2005) p.366
↑ Gille & Szamuely (2006) p.184
↑ Lam (2005) p.316

Gille, Philippe; Szamuely, Tamás (2006). Central simple algebras and Galois cohomology. Cambridge Studies in Advanced Mathematics 101. Cambridge: Cambridge University Press. ISBN 0-521-86103-9. Zbl 1137.12001.
Lam, Tsit-Yuen (2005). Introduction to Quadratic Forms over Fields. Graduate Studies in Mathematics 67. American Mathematical Society. ISBN 0-8218-1095-2. MR 2104929. Zbl 1068.11023.
Milnor, John Willard (1970), With an appendix by J. Tate, "Algebraic K-theory and quadratic forms", Inventiones Mathematicae 9: 318–344, doi:10.1007/BF01425486, ISSN 0020-9910, MR 0260844, Zbl 0199.55501

Milnor K-theory

Definition

Examples

Applications

References

Further reading