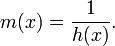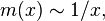Mills ratio
In probability theory, the Mills ratio (or Mills's ratio[1]) of a continuous random variable  is the function
is the function
where 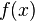 is the probability density function, and
is the probability density function, and
is the complementary cumulative distribution function (also called survival function). The concept is named after John P. Mills. The Mills ratio is related[2] to the hazard rate h(x) which is defined as
by
Example
If  has standard normal distribution then
has standard normal distribution then
where the sign 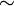 means that the quotient of the two functions converges to 1 as
means that the quotient of the two functions converges to 1 as 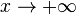 . More precise asymptotics can be given.[3]
. More precise asymptotics can be given.[3]
See also
References
- ↑ G. Grimmett, S. Stirzaker. Probability Theory and Random Processes. 3rd ed. Cambridge. Page 98.
- ↑ Klein, J.P., Moeschberger, M.L.: Survival Analysis: Techniques for Censored and Truncated Data, Springer, 2003, p.27
- ↑ Small, Christopher G. (2010), Expansions and Asymptotics for Statistics, Monographs on Statistics & Applied Probability 115, CRC Press, pp. 48, 50–51, 88–90, ISBN 9781420011029.
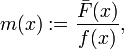
![\bar{F}(x) := \Pr[X>x] = \int_x^{+\infty} f(u)\, du](../I/m/d4b3981c0e2ea25169477aec6169a411.png)
![h(x):=\lim_{\delta\to 0} \frac{1}{\delta}\Pr[x < X \leq x + \delta | X > x]](../I/m/af3f744871fbb9695c60f3bd9fd2ceff.png)