Milliken's tree theorem

In mathematics, Milliken's tree theorem in combinatorics is a partition theorem generalizing Ramsey's theorem to infinite trees, objects with more structure than sets.

Let T be a finitely splitting rooted tree of height ω, n a positive integer, and 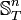$\mathbb{S}^n_T$ the collection of all strongly embedded subtrees of T of height n. In one of its simple forms, Milliken's tree theorem states that if 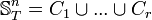$\mathbb{S}^n_T=C_1 \cup ... \cup C_r$ then for some strongly embedded infinite subtree R of T, 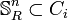$\mathbb{S}^n_R \subset C_i$ for some i ≤ r.

This immediately implies Ramsey's theorem; take the tree T to be a linear ordering on ω vertices.

Define 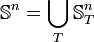$\mathbb{S}^n= \bigcup_T \mathbb{S}^n_T$ where T ranges over finitely splitting rooted trees of height ω. Milliken's tree theorem says that not only is 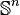$\mathbb{S}^n$ partition regular for each n < ω, but that the homogeneous subtree R guaranteed by the theorem is strongly embedded in T.

Strong embedding

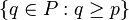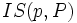Call T an α-tree if each branch of T has cardinality α. Define Succ(p, P)= $\{ q \in P : q \geq p \}$ , and $IS(p,P)$ to be the set of immediate successors of p in P. Suppose S is an α-tree and T is a β-tree, with 0 ≤ α ≤ β ≤ ω. S is strongly embedded in T if:

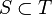$S \subset T$ , and the partial order on S is induced from T,
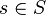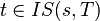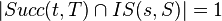if $s \in S$ is nonmaximal in S and $t \in IS(s,T)$ , then $|Succ(t,T) \cap IS(s,S)|=1$ ,
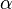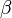there exists a strictly increasing function from $\alpha$ to $\beta$ , such that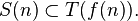 $S(n) \subset T(f(n)).$

Intuitively, for S to be strongly embedded in T,

S must be a subset of T with the induced partial order
S must preserve the branching structure of T; i.e., if a nonmaximal node in S has n immediate successors in T, then it has n immediate successors in S
S preserves the level structure of T; all nodes on a common level of S must be on a common level in T.

References

Keith R. Milliken, A Ramsey Theorem for Trees J. Comb. Theory (Series A) 26 (1979), 215-237
Keith R. Milliken, A Partition Theorem for the Infinite Subtrees of a Tree, Trans. Amer. Math. Soc. 263 No.1 (1981), 137-148.