Michael Shub

Michael Shub

Michael Shub in April 2012
Born Michael Ira Shub
August 17, 1943
Nationality USA
Alma mater University of California, Berkeley
Occupation mathematician, professor
Known for Blum Blum Shub pseudorandom number generator

Michael Ira Shub (born August 17, 1943) is an American mathematician who has done research into Dynamical Systems and the Complexity of Real Number Algorithms.

Biography

Shub obtained his Ph.D. degree at the University of California, Berkeley with a thesis entitled Endomorphisms of Compact Differentiable Manifolds on 1967. His advisor was Stephen Smale.[1] From 1967 to 1985 he worked at Brandeis University, the University of California (Santa Cruz) and the Queens College at the City University of New York. From 1985 to 2004 he joined IBM's Thomas J. Watson Research Center. From 2004 to 2010 he worked at the University of Toronto. After 2010 he is a researcher at the University of Buenos Aires and at the City University of New York.

In 2012, a conference From Dynamics to Complexity was organised at the Fields Institute in Toronto celebrating his work.[2]

Work

Shub has produced important publications in Dynamical Systems and in the Complexity of Real Number Algorithms. In his Ph.D. in 1967 he introduced the notion of expanding maps, which gave the first examples of structurally stable strange attractors. In 1974 he proposed the Entropy Conjecture, an important open problem in Dynamical Systems, which was proved by Yosef Yomdin for 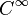C^\infty mappings in 1987.[3] This same year Michael Shub published his book Global Stability of Dynamical Systems, which is often used as a reference in introductory and advances books on the subject of Dynamical Systems.[4][5][6] He described jointly with Lenore and Manuel Blum a simple, unpredictable, secure random number generator, see Blum Blum Shub, which is considered an important landmark both from theoretical and practical perspectives, see.[7] In 1989 he proposed with Lenore Blum and Stephen Smale the notion of Blum–Shub–Smale machine, an alternative to the classical Turing model of computation. Their model became an extremely important tool to analyse the computability of functions.[8] In 1993, Shub and Smale initiated a rigurous analysis of homotopy-based algorithms for solving systems of nonlinear algebraic equations which has inspired much of the work in that area during the last two decades.[9] Shub was one of the founders of the nonprofit association Foundations of Computational Mathematics, and editor of their journal Foundations of Computational Mathematics with the same name until 2009.

Selected publications

Blum, Lenore; Blum, Manuel; Shub, (1 May 1986). "A Simple Unpredictable Pseudo-Random Number Generator". SIAM Journal on Computing 15 (2): 364–383. doi:10.1137/0215025.

M. Shub, Dynamical Systems, filtrations and entropy, Bulletin of the American Mathematical Society 80, 1974, pp. 27–41.

M. Shub, Global Stability of Dynamical Systems, Springer-Berlag: New York, Heidelberg, Berlin, 1987.

L. Blum, M. Shub and S. Smale, On a theory of computation and complexity over the real numbers: NP-completeness, recursive functions and universal machines, Bulletin of the American Mathematical Society, juillet 1989.

M. Shub and S. Smale Complexity of Bezout's Theorem I: Geometric Aspects, Journal of the American Mathematical Society, volume 6, number 2, 1993.

L. Blum, F. Cucker, M. Shub and S. Smale Complexity and Real Computation Springer-Berlag: New York, Heidelberg, Berlin, 1997.

References

  1. ↑ Michael Ira Shub at the Mathematics Genealogy Project
  2. ↑ From Dynamics to Complexity - A conference celebrating the work of Shub
  3. ↑ Y. Yomdin, Volume growth and entropy., Israel J. Math. 57, no. 3, 1987.
  4. ↑ Devaney, R. A first course in chaotic dynamical systems, Westview Press, 1992.
  5. ↑ Wiggins, S. Introduction to applied nonlinear systems and chaos, Springer, 1990.
  6. ↑ Hasselblatt , B. and Katok, A. Handbook of dynamical systems, Vol I, Elsevier, 2002.
  7. ↑ Stinson, D. Cryptography: Theory and Practice, Third Edition, Taylor and Francis, 2005
  8. ↑ Gradel, E. Finite Model Theory and Its Applications, Springer-Verlag, 2007
  9. ↑ Bürgisser, P. and Cucker, F.Condition: The Geometry of Numerical Algorithms, Springer, 2013

External links