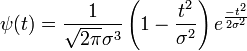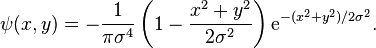Mexican hat wavelet

Mexican hat

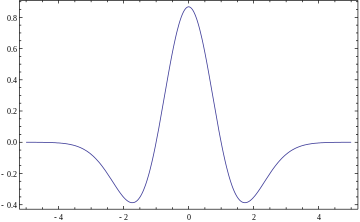
In mathematics and numerical analysis, the Ricker wavelet[1]

\psi(t) = {1 \over {\sqrt {2\pi}\sigma^3}} \left( 1 - {t^2 \over \sigma^2} \right) e^{-t^2 \over 2\sigma^2}

is the negative normalized second derivative of a Gaussian function, i.e., up to scale and normalization, the second Hermite function. It is a special case of the family of continuous wavelets (wavelets used in a continuous wavelet transform) known as Hermitian wavelets. The Ricker wavelet is frequently employed to model seismic data, and as a broad spectrum source term in computational electrodynamics. It is usually only referred to as the Mexican hat wavelet in the Americas, due to taking the shape of a sombrero when used as a 2D image processing kernel. It is also known as the Marr wavelet for David Marr.[2][3]

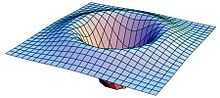
\psi(x,y) = -\frac{1}{\pi\sigma^4}\left(1-\frac{x^2+y^2}{2\sigma^2}\right) \mathrm{e}^{-(x^2+y^2)/2\sigma^2}.
3D Mexican hat wavelet

The multidimensional generalization of this wavelet is called the Laplacian of Gaussian function. In practice, this wavelet is sometimes approximated by the difference of Gaussians function, because it is separable[4] and can therefore save considerable computation time in two or more dimensions. The scale normalised Laplacian (in 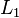L_1-norm) is frequently used as a blob detector and for automatic scale selection in computer vision applications; see Laplacian of Gaussian and scale space. The Mexican hat wavelet can also be approximated by derivatives of Cardinal B-Splines[5]

References

  1. ↑ http://74.3.176.63/publications/recorder/1994/09sep/sep94-choice-of-wavelets.pdf
  2. ↑ http://www2.isye.gatech.edu/~brani/isyebayes/bank/handout20.pdf
  3. ↑ http://cxc.harvard.edu/ciao/download/doc/detect_manual/wav_theory.html#wav_theory_mh
  4. ↑ Fisher, Perkins, Walker and Wolfart. "Spatial Filters - Gaussian Smoothing". Retrieved 23 February 2014.
  5. ↑ Brinks R: On the convergence of derivatives of B-splines to derivatives of the Gaussian function, Comp. Appl. Math., 27, 1, 2008