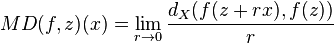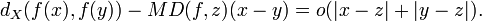Metric differential

In mathematical analysis, a metric differential is a generalization of a derivative for a Lipschitz continuous function defined on a Euclidean space and taking values in an arbitrary metric space. With this definition of a derivative, one can generalize Rademarcher's theorem to metric space-valued Lipschitz functions.

Discussion

Rademacher's theorem states that a Lipschitz map f : Rn → Rm is differentiable almost everywhere in Rn; in other words, for almost every x, f is approximately linear in any sufficiently small range of x. If f is a function from a Euclidean space Rn that takes values instead in a metric space X, it doesn't immediately make sense to talk about differentiability since X has no linear structure a priori. Even if you assume that X is a Banach space and ask whether a Fréchet derivative exists almost everywhere, this does not hold. For example, consider the function f : [0,1] → L1([0,1]), mapping the unit interval into the space of integrable functions, defined by f(x) = χ[0,x], this function is Lipschitz (and in fact, an isometry) since, if 0 ≤ x ≤ y≤ 1, then

|f(x)-f(y)|=\int_0^1 |\chi_{[0,x]}(t)-\chi_{[0,y]}(t)|\,dt = \int_x^y \, dt = |x-y|,

but one can verify that limh→0(f(x + h) −  f(x))/h does not converge to an L1 function for any x in [0,1], so it is not differentiable anywhere.

However, if you look at Rademacher's theorem as a statement about how a Lipschitz function stabilizes as you zoom in on almost every point, then such a theorem exists but is stated in terms of the metric properties of f instead of its linear properties.

Definition and existence of the metric differential

A substitute for a derivative of f:Rn → X is the metric differential of f at a point z in Rn which is a function on Rn defined by the limit

MD(f,z)(x)=\lim_{r\rightarrow 0} \frac{d_{X}(f(z+rx),f(z))}{r}

whenever the limit exists (here d X denotes the metric on X).

A theorem due to Bernd Kirchheim[1] states that a Rademacher theorem in terms of metric differentials holds: for almost every z in Rn, MD(f, z) is a seminorm and

d_X(f(x),f(y)) - MD(f,z)(x-y) = o(|x-z|+|y-z|). \,

The little-o notation employed here means that, at values very close to z, the function f is approximately an isometry from Rn with respect to the seminorm MD(f, z) into the metric space X.

References

  1. ↑ Kirchheim, Bernd (1994). "Rectifiable metric spaces: local structure and regularity of the Hausdorff measure". Proc. of the Am. Math. Soc. 121: 113–124.