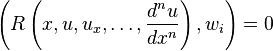Method of mean weighted residuals

In applied mathematics, methods of mean weighted residuals (MWR) are methods for solving differential equations. The solutions of these differential equations are assumed to be well approximated by a finite sum of test functions 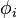$\phi_i$ . In such cases, any one of a theoretically infinite set of methods of weighted residuals (depending on the choice of 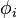$\phi_i$ ) are applied in an attempt to find which precise value each of the coefficient weight of the corresponding test functions. These coefficients are made to minimize the error between the sum of the test functions and actual solution in a chosen norm.

Notation of this page

It is often very important to firstly sort out notation used before presenting how this method is executed in order to avoid confusion.

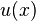$u(x)$ shall be used to denote the solution to the differential equation that the MWR method is being applied to.
Solving the differential equation mentioned shall be set to equate to setting some function 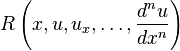$R\left(x,u,u_x,\ldots,\frac{d^n u}{dx^n}\right)$ called the "residue function" to zero.
Every method of mean weighted residuals involves some "test functions" that shall be denoted by $w_i$ .
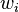The degrees of freedom shall be denoted by $a_i$ .
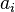If the assumed form of the solution to the differential equation 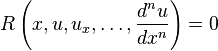$R\left(x,u,u_x,\ldots,\frac{d^n u}{dx^n}\right)=0$ is linear (in the degrees of freedom) then the basis functions used in said form shall be denoted by $\phi_i$ .

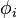Mathematical statement of method

The method of mean weighted residuals solves 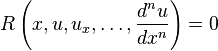$R\left(x,u,u_x,\ldots,\frac{d^n u}{dx^n}\right)=0$ by imposing that the degrees of freedom 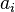$a_i$ are such that:

\left(R\left(x,u,u_x,\ldots,\frac{d^n u}{dx^n}\right),w_i\right)=0

is satisfied. Where the inner product 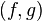$(f,g)$ is the standard function inner product with respect to some weighting function 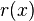$r(x)$ which is determined usually by the basis function set or arbitrarily according to whichever weighting function is most convenient. For instance when the basis set is just the Chebyshev polynomials of the first kind typically the weighting function is 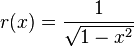$r(x)=\frac{1}{\sqrt{1-x^2}}$ because that's the most convenient because that way inner products can be more easily computed by use of a fast Chebyshev transform.

Additionally, all these methods have in common that they enforce boundary conditions by either enforcing that the basis functions (in the case of a linear combination) individual enforce the boundary conditions on the original BVP (This only works if the boundary conditions are homogeneous however it is possible to apply it to problems with inhomogeneous boundary conditions by letting 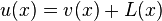$u(x)=v(x)+L(x)$ and substituting this expression into the original differential equation and imposing homogeneous boundary conditions to the new solution being sought to find u(x) that is v(x) where L(x) is a function that satisfies the boundary conditions imposed on u that is known.), or by explicitly imposing the boundary by removing n rows to the matrix representing the discretised problem where n refers to the order of the differential equation and substituting them with ones that represent the boundary conditions.

Choice of test functions

The choice of test function, as mentioned earlier, depends on the specific method used (under the general heading of mean weighted residual methods). Here is a list of commonly used specific MWR methods and their corresponding test functions roughly according to their popularity:

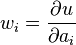
The Galerkin method, which uses the basis functions themselves as test functions or in the more general case of a nonlinear assumed form (where the nonlinearity is in the degrees of freedom) of the solution the Galerkin method uses the test functions: $w_i =\frac{\partial u}{\partial a_i}$
The pseudospectral method which uses the Dirac delta functions centered at a set of discrete x points 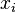$x_i$ and equates to just setting the residue function to zero at those x points.
The least-squares method uses the test functions: 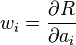$w_i =\frac{\partial R}{\partial a_i}$ . This method has the effect of minimising the square of the L2-norm of the residue function (that is 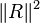$\|{R}\|^2$ ) with respect to the degrees of freedom $a_i$ .
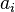The method of moments uses the simple set of test functions 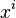$x^i$ and is rarely ever implemented when high degrees of accuracy are required because of computational issues associated with inverting the Hilbert matrix.

References

Introduction to Applied Mathematics, Wellesley-Cambridge Press (1986).