Metaplectic structure

In differential geometry, a metaplectic structure is the symplectic analog of spin structure on orientable Riemannian manifolds. A metaplectic structure on a symplectic manifold allows one to define the symplectic spinor bundle, which is the Hilbert space bundle associated to the metaplectic structure via the metaplectic representation, giving rise to the notion of a symplectic spinor field in differential geometry.

Symplectic spin structures have wide applications to mathematical physics, in particular to quantum field theory where they are an essential ingredient in establishing the idea that symplectic spin geometry and symplectic Dirac operators may give valuable tools in symplectic geometry and symplectic topology. They are also of purely mathematical interest in differential geometry, algebraic topology, and K theory. They form the foundation for symplectic spin geometry.

Formal definition

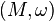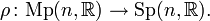A metaplectic structure ^[1] on a symplectic manifold $(M, \omega)$ is an equivariant lift of the symplectic frame bundle $\pi_{\mathbf R}\colon{\mathbf R}\to M\,$ with respect to the double covering $\rho\colon {\mathrm {Mp}}(n,{\mathbb R})\to {\mathrm {Sp}}(n,{\mathbb R}).\,$ In other words, a pair $({\mathbf P},F_{\mathbf P})$ is a metaplectic structure on the principal bundle $\pi_{\mathbf R}\colon{\mathbf R}\to M\,$ when

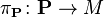\pi_{\mathbf P}\colon{\mathbf P}\to M\,

is a principal

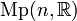{\mathrm {Mp}}(n,{\mathbb R})

-bundle over

M

F_{\mathbf P}\colon{\mathbf P}\to {\mathbf R}\,

is an equivariant

2

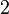-fold covering map such that

\pi_{\mathbf R}\circ F_{\mathbf P}=\pi_{\mathbf P}

and

F_{\mathbf P}({\mathbf p}q)=F_{\mathbf P}({\mathbf p})\rho(q)

for all

{\mathbf p}\in {\mathbf P}

and

q\in {\mathrm {Mp}}(n,{\mathbb R}).

The principal bundle 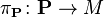$\pi_{\mathbf P}\colon{\mathbf P}\to M\,$ is also called the bundle of metaplectic frames over $M$ .

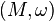Two metaplectic structures $({\mathbf P_1},F_{\mathbf P_1})$ and $({\mathbf P_2},F_{\mathbf P_2})$ on the same symplectic manifold $(M, \omega)$ are called equivalent if there exists a 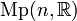${\mathrm {Mp}}(n,{\mathbb R})$ -equivariant map $f\colon {\mathbf P_1}\to {\mathbf P_2}$ such that

F_{\mathbf P_2}\circ f=F_{\mathbf P_1}

and

f({\mathbf p}q)=f({\mathbf p})q

for all

{\mathbf p}\in {\mathbf P_1}

and

q\in {\mathrm {Mp}}(n,{\mathbb R}).

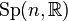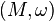Of course, in this case $F_{\mathbf P_1}$ and $F_{\mathbf P_2}$ are two equivalent double coverings of the symplectic frame ${\mathrm {Sp}}(n,{\mathbb R})$ -bundle $\pi_{\mathbf R}\colon{\mathbf R}\to M\,$ of the given symplectic manifold $(M, \omega)$ .

Obstruction

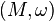Since every symplectic manifold $M$ is necessarily of even dimension and orientable, one can prove that the topological obstruction to the existence of metaplectic structures is precisely the same as in Riemannian spin geometry.^[2] In other words, a symplectic manifold $(M, \omega)$ admits a metaplectic structures if and only if the second Stiefel-Whitney class $w_2(M)\in H^2(M,{\mathbb Z_2})$ of $M$ vanishes. In fact, the modulo $_2$ reduction of the first Chern class $c_1(M)\in H^2(M,{\mathbb Z})$ is the second Stiefel-Whitney class $w_2(M)$ . 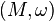Hence, $(M, \omega)$ admits metaplectic structures if and only if $c_1(M)$ is even, i.e., if and only if $w_2(M)$ is zero.

If this is the case, the isomorphy classes of metaplectic structures on 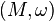$(M, \omega)$ are classified by the first cohomology group $H^1(M,{\mathbb Z_2})$ of $M$ with ${\mathbb Z_2}$ -coefficients.

As the manifold $M$ is assumed to be oriented, the first Stiefel-Whitney class $w_1(M)\in H^1(M,{\mathbb Z_2})$ of $M$ vanishes too.

Examples

Manifolds admitting a metaplectic structure

Phase spaces $(T^{\ast}N,\theta)\, ,$ $N$ any orientable manifold.
Complex projective spaces ${\mathbb P}^{2k+1}{\mathbb C}\, ,$ $\, k\in {\mathbb N}_{0}\, .$ Since ${\mathbb P}^{2k+1}{\mathbb C}\,$ is simply connected, such a structure has to be unique.
Grassmannian $Gr(2,4)\, ,$ e.t.c.

Notes

↑ Habermann, Katharina; Habermann, Lutz (2006), Introduction to Symplectic Dirac Operators, Springer-Verlag, ISBN 978-3-540-33420-0 page 35
↑ M. Forger, H. Hess (1979). "Universal metaplectic structures and geometric quantization". Commun. Math. Phys. 64: 269–278. doi:10.1007/bf01221734.

References

Habermann, Katharina; Habermann, Lutz (2006), Introduction to Symplectic Dirac Operators, Springer-Verlag, ISBN 978-3-540-33420-0
Hassan, Jolany. "Metaplectic Quantization".