Metabolic network modelling

Metabolic network reconstruction and simulation allows for an in-depth insight into the molecular mechanisms of a particular organism. In particular, these models correlate the genome with molecular physiology.[1] A reconstruction breaks down metabolic pathways (such as glycolysis and the Citric acid cycle) into their respective reactions and enzymes, and analyzes them within the perspective of the entire network. In simplified terms, a reconstruction collects all of the relevant metabolic information of an organism and compiles it in a mathematical model. Validation and analysis of reconstructions can allow identification of key features of metabolism such as growth yield, resource distribution, network robustness, and gene essentiality. This knowledge can then be applied to create novel biotechnology.
In general, the process to build a reconstruction is as follows:
- Draft a reconstruction
- Refine the model
- Convert model into a mathematical/computational representation
- Evaluate and debug model through experimentation
Genome-Scale Metabolic Reconstruction
A metabolic reconstruction provides a highly mathematical, structured platform on which to understand the systems biology of metabolic pathways within an organism.[2] The integration of biochemical metabolic pathways with rapidly available, unannotated genome sequences has developed what are called genome-scale metabolic models. Simply put, these models correspond metabolic genes with metabolic pathways. In general, the more information about physiology, biochemistry and genetics is available for the target organism, the better the predictive capacity of the reconstructed models. Mechanically speaking, the process of reconstructing prokaryotic and eukaryotic metabolic networks is essentially the same. Having said this, eukaryote reconstructions are typically more challenging because of the size of genomes, coverage of knowledge, and the multitude of cellular compartments.[2] The first genome-scale metabolic model was generated in 1995 for Haemophilus influenzae.[3] The first multicellular organism, C. elegans, was reconstructed in 1998.[4] Since then, many reconstructions have been formed. For a list of reconstructions that have been converted into a model and experimentally validated, see http://sbrg.ucsd.edu/InSilicoOrganisms/OtherOrganisms.
| Organism | Genes in Genome | Genes in Model | Reactions | Metabolites | Date of reconstruction | Reference |
|---|---|---|---|---|---|---|
| Haemophilus influenzae | 1,775 | 296 | 488 | 343 | June 1999 | [3] |
| Escherichia coli | 4,405 | 660 | 627 | 438 | May 2000 | [5] |
| Saccharomyces cerevisiae | 6,183 | 708 | 1,175 | 584 | February 2003 | [6] |
| Mus musculus | 28,287 | 473 | 1220 | 872 | January 2005 | [7] |
| Homo sapiens | 21,090[8] | 3,623 | 3,673 | -- | January 2007 | [9] |
| Mycobacterium tuberculosis | 4,402 | 661 | 939 | 828 | June 2007 | [10] |
| Bacillus subtilis | 4,114 | 844 | 1,020 | 988 | September 2007 | [11] |
| Synechocystis sp. PCC6803 | 3,221 | 633 | 831 | 704 | October 2008 | [12] |
| Salmonella typhimurium | 4,489 | 1,083 | 1,087 | 774 | April 2009 | [13] |
| Arabidopsis thaliana | 27,379 | 1,419 | 1,567 | 1,748 | February 2010 | [14] |
Drafting a reconstruction
Resources
Because the timescale for the development of reconstructions is so recent, most reconstructions have been built manually. However, now, there are quite a few resources that allow for the semi-automatic assembly of these reconstructions that are utilized due to the time and effort necessary for a reconstruction. An initial fast reconstruction can be developed automatically using resources like PathoLogic or ERGO in combination with encyclopedias like MetaCyc, and then manually updated by using resources like PathwayTools. These semi-automatic methods allow for a fast draft to be created while allowing the fine tune adjustments required once new experimental data is found. It is only in this manner that the field of metabolic reconstructions will keep up with the ever-increasing numbers of annotated genomes.
Databases
- Kyoto Encyclopedia of Genes and Genomes (KEGG): a bioinformatics database containing information on genes, proteins, reactions, and pathways. The ‘KEGG Organisms’ section, which is divided into eukaryotes and prokaryotes, encompasses many organisms for which gene and DNA information can be searched by typing in the enzyme of choice.
- BioCyc, EcoCyc, and MetaCyc: BioCyc Is a collection of 3,000 pathway/genome databases (as of Oct 2013), with each database dedicated to one organism. For example, EcoCyc is a highly detailed bioinformatics database on the genome and metabolic reconstruction of Escherichia coli, including thorough descriptions of E. coli signaling pathways and regulatory network. The EcoCyc database can serve as a paradigm and model for any reconstruction. Additionally, MetaCyc, an encyclopedia of experimentally defined metabolic pathways and enzymes, contains 2,100 metabolic pathways and 11,400 metabolic reactions (Oct 2013).
- ENZYME: An enzyme nomenclature database (part of the ExPASy proteonomics server of the Swiss Institute of Bioinformatics). After searching for a particular enzyme on the database, this resource gives you the reaction that is catalyzed. ENZYME has direct links to other gene/enzyme/literature databases such as KEGG, BRENDA, and PUBMED.
- BRENDA: A comprehensive enzyme database that allows for an enzyme to be searched by name, EC number, or organism.
- BiGG: A knowledge base of biochemically, genetically, and genomically structured genome-scale metabolic network reconstructions.
- metaTIGER: Is a collection of metabolic profiles and phylogenomic information on a taxonomically diverse range of eukaryotes which provides novel facilities for viewing and comparing the metabolic profiles between organisms.
| Database | Scope | ||||
|---|---|---|---|---|---|
| Enzymes | Genes | Reactions | Pathways | Metabolites | |
| KEGG | X | X | X | X | X |
| BioCyc | X | X | X | X | X |
| MetaCyc | X | X | X | X | |
| ENZYME | X | X | X | ||
| BRENDA | X | X | X | ||
| BiGG | X | X | X | ||
Tools for Metabolic Modeling
- Pathway Tools: A bioinformatics software package that assists in the construction of pathway/genome databases such as EcoCyc.[15] Developed by Peter Karp and associates at the SRI International Bioinformatics Research Group, Pathway Tools has several components. Its PathoLogic module takes an annotated genome for an organism and infers probable metabolic reactions and pathways to produce a new pathway/genome database. Its MetaFlux component can generate a quantitative metabolic model from that pathway/genome database using flux-balance analysis. Its Navigator component provides extensive query and visualization tools, such as visualization of metabolites, pathways, and the complete metabolic network.
- ERGO: A subscription-based service developed by Integrated Genomics. It integrates data from every level including genomic, biochemical data, literature, and high-throughput analysis into a comprehensive user friendly network of metabolic and nonmetabolic pathways.
- KEGGtranslator:[16][17] an easy-to-use stand-alone application that can visualize and convert KEGG files (KGML formatted XML-files) into multiple output formats. Unlike other translators, KEGGtranslator supports a plethora of output formats, is able to augment the information in translated documents (e.g., MIRIAM annotations) beyond the scope of the KGML document, and amends missing components to fragmentary reactions within the pathway to allow simulations on those. KEGGtranslator converts these files to SBML, BioPAX, SIF, SBGN, SBML with qualitative modeling extension,[18] GML, GraphML, JPG, GIF, LaTeX, etc.
KEGG pathways can directly be obtained from within the application.
- Model SEED: An online resource for the analysis, comparison, reconstruction, and curation of genome-scale metabolic models.[19] Users can submit genome sequences to the RAST annotation system, and the resulting annotation can be automatically piped into the Model SEED to produce a draft metabolic model. The Model SEED automatically constructs a network of metabolic reactions, gene-protein-reaction associations for each reaction, and a biomass composition reaction for each genome to produce a model of microbial metabolism that can be simulated using Flux Balance Analysis.
- MetaMerge: algorithm for semi-automatically reconciling a pair of existing metabolic network reconstructions into a single metabolic network model.[20]
Tools for Literature
- PUBMED: This is an online library developed by the National Center for Biotechnology Information, which contains a massive collection of medical journals. Using the link provided by ENZYME, the search can be directed towards the organism of interest, thus recovering literature on the enzyme and its use inside of the organism.
Methodology to draft a reconstruction
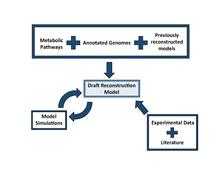
A reconstruction is built by compiling data from the resources above. Database tools such as KEGG and BioCyc can be used in conjunction with each other to find all the metabolic genes in the organism of interest. These genes will be compared to closely related organisms that have already developed reconstructions to find homologous genes and reactions. These homologous genes and reactions are carried over from the known reconstructions to form the draft reconstruction of the organism of interest. Tools such as ERGO, Pathway Tools and Model SEED can compile data into pathways to form a network of metabolic and non-metabolic pathways. These networks are then verified and refined before being made into a mathematical simulation.[2]
The predictive aspect of a metabolic reconstruction hinges on the ability to predict the biochemical reaction catalyzed by a protein using that protein's amino acid sequence as an input, and to infer the structure of a metabolic network based on the predicted set of reactions. A network of enzymes and metabolites is drafted to relate sequences and function. When an uncharacterized protein is found in the genome, its amino acid sequence is first compared to those of previously characterized proteins to search for homology. When a homologous protein is found, the proteins are considered to have a common ancestor and their functions are inferred as being similar. However, the quality of a reconstruction model is dependent on its ability to accurately infer phenotype directly from sequence, so this rough estimation of protein function will not be sufficient. A number of algorithms and bioinformatics resources have been developed for refinement of sequence homology-based assignments of protein functions:
- InParanoid: Identifies eukaryotic orthologs by looking only at in-paralogs.
- CDD: Resource for the annotation of functional units in proteins. Its collection of domain models utilizes 3D structure to provide insights into sequence/structure/function relationships.
- InterPro: Provides functional analysis of proteins by classifying them into families and predicting domains and important sites.
- STRING: Database of known and predicted protein interactions.
Once proteins have been established, more information about the enzyme structure, reactions catalyzed, substrates and products, mechanisms, and more can be acquired from databases such as KEGG, MetaCyc and NC-IUBMB. Accurate metabolic reconstructions require additional information about the reversibility and preferred physiological direction of an enzyme-catalyzed reaction which can come from databases such as BRENDA or MetaCyc database.[21]
Model Refinement
An initial metabolic reconstruction of a genome is typically far from perfect due to the high variability and diversity of microorganisms. Often, metabolic pathway databases such as KEGG and MetaCyc will have "holes", meaning that there is a conversion from a substrate to a product (i.e., an enzymatic activity) for which there is no known protein in the genome that encodes the enzyme that facilitates the catalysis. What can also happen in semi-automatically drafted reconstructions is that some pathways are falsely predicted and don't actually occur in the predicted manner.[21] Because of this, a systematic verification is made in order to make sure no inconsistencies are present and that all the entries listed are correct and accurate.[1] Furthermore, previous literature can be researched in order to support any information obtained from one of the many metabolic reaction and genome databases. This provides an added level of assurance for the reconstruction that the enzyme and the reaction it catalyzes do actually occur in the organism.
Any new reactions not present in the databases need to be added to the reconstruction. This is an iterative process that cycles between the experimental phase and the coding phase. As new information is found about the target organism, the model will be adjusted to predict the metabolic and phenotypical output of the cell. The presence or absence of certain reactions of the metabolism will affect the amount of reactants/products that are present for other reactions within the particular pathway. This is because products in one reaction go on to become the reactants for another reaction, i.e. products of one reaction can combine with other proteins or compounds to form new proteins/compounds in the presence of different enzymes or catalysts.[1]
Francke et al. [1] provide an excellent example as to why the verification step of the project needs to be performed in significant detail. During a metabolic network reconstruction of Lactobacillus plantarum, the model showed that succinyl-CoA was one of the reactants for a reaction that was a part of the biosynthesis of methionine. However, an understanding of the physiology of the organism would have revealed that due to an incomplete tricarboxylic acid pathway, Lactobacillus plantarum does not actually produce succinyl-CoA, and the correct reactant for that part of the reaction was acetyl-CoA.
Therefore, systematic verification of the initial reconstruction will bring to light several inconsistencies that can adversely affect the final interpretation of the reconstruction, which is to accurately comprehend the molecular mechanisms of the organism. Furthermore, the simulation step also ensures that all the reactions present in the reconstruction are properly balanced. To sum up, a reconstruction that is fully accurate can lead to greater insight about understanding the functioning of the organism of interest.[1]
Metabolic network simulation
A metabolic network can be broken down into a stoichiometric matrix where the rows represent the compounds of the reactions, while the columns of the matrix correspond to the reactions themselves. Stoichiometry is a quantitative relationship between substrates of a chemical reaction. In order to deduce what the metabolic network suggests, recent research has centered on a few approaches, such as extreme pathways, elementary mode analysis,[22] flux balance analysis, and a number of other constraint-based modeling methods.[23][24]
Extreme Pathways
Price,[25] from the Palsson lab, uses a method of singular value decomposition (SVD) of extreme pathways in order to understand regulation of a human red blood cell metabolism. Extreme pathways are convex basis vectors that consist of steady state functions of a metabolic network.[26] For any particular metabolic network, there is always a unique set of extreme pathways available.[27] Furthermore, Price[25] defines a constraint-based approach, where through the help of constraints like mass balance and maximum reaction rates, it is possible to develop a ‘solution space’ where all the feasible options fall within. Then, using a kinetic model approach, a single solution that falls within the extreme pathway solution space can be determined.[25] Therefore, in their study, Price [25] uses both constraint and kinetic approaches to understand the human red blood cell metabolism. In conclusion, using extreme pathways, the regulatory mechanisms of a metabolic network can be studied in further detail.
Elementary mode analysis
Elementary mode analysis closely matches the approach used by extreme pathways. Similar to extreme pathways, there is always a unique set of elementary modes available for a particular metabolic network.[27] These are the smallest sub-networks that allow a metabolic reconstruction network to function in steady state.[28][29] According to Stelling (2002),[29] elementary modes can be used to understand cellular objectives for the overall metabolic network. Furthermore, elementary mode analysis takes into account stoichiometrics and thermodynamics when evaluating whether a particular metabolic route or network is feasible and likely for a set of proteins/enzymes.[28]
Minimal metabolic behaviors (MMBs)
In 2009, Larhlimi and Bockmayr presented a new approach called "minimal metabolic behaviors" for the analysis of metabolic networks.[30] Like elementary modes or extreme pathways, these are uniquely determined by the network, and yield a complete description of the flux cone. However, the new description is much more compact. In contrast with elementary modes and extreme pathways, which use an inner description based on generating vectors of the flux cone, MMBs are using an outer description of the flux cone. This approach is based on sets of non-negativity constraints. These can be identified with irreversible reactions, and thus have a direct biochemical interpretation. One can characterize a metabolic network by MMBs and the reversible metabolic space.
Flux balance analysis
A different technique to simulate the metabolic network is to perform flux balance analysis. This method uses linear programming, but in contrast to elementary mode analysis and extreme pathways, only a single solution results in the end. Linear programming is usually used to obtain the maximum potential of the objective function that you are looking at, and therefore, when using flux balance analysis, a single solution is found to the optimization problem.[29] In a flux balance analysis approach, exchange fluxes are assigned to those metabolites that enter or leave the particular network only. Those metabolites that are consumed within the network are not assigned any exchange flux value. Also, the exchange fluxes along with the enzymes can have constraints ranging from a negative to positive value (ex: -10 to 10).
Furthermore, this particular approach can accurately define if the reaction stoichiometry is in line with predictions by providing fluxes for the balanced reactions. Also, flux balance analysis can highlight the most effective and efficient pathway through the network in order to achieve a particular objective function. In addition, gene knockout studies can be performed using flux balance analysis. The enzyme that correlates to the gene that needs to be removed is given a constraint value of 0. Then, the reaction that the particular enzyme catalyzes is completely removed from the analysis.
Dynamic simulation and parameter estimation
In order to perform a dynamic simulation with such a network it is necessary to construct an ordinary differential equation system that describes the rates of change in each metabolite's concentration or amount. To this end, a rate law, i.e., a kinetic equation that determines the rate of reaction based on the concentrations of all reactants is required for each reaction. Software packages that include numerical integrators, such as COPASI or SBMLsimulator, are then able to simulate the system dynamics given an initial condition. Often these rate laws contain kinetic parameters with uncertain values. In many cases it is desired to estimate these parameter values with respect to given time-series data of metabolite concentrations. The system is then supposed to reproduce the given data. For this purpose the distance between the given data set and the result of the simulation, i.e., the numerically or in few cases analytically obtained solution of the differential equation system is computed. The values of the parameters are then estimated to minimize this distance.[31] One step further, it may be desired to estimate the mathematical structure of the differential equation system because the real rate laws are not known for the reactions within the system under study. To this end, the program SBMLsqueezer allows automatic creation of appropriate rate laws for all reactions with the network. [32]
Synthetic Accessibility
Synthetic accessibility is a simple approach to network simulation whose goal is to predict which metabolic gene knockouts are lethal. The synthetic accessibility approach uses the topology of the metabolic network to calculate the sum of the minimum number of steps needed to traverse the metabolic network graph from the inputs, those metabolites available to the organism from the environment, to the outputs, metabolites needed by the organism to survive. To simulate a gene knockout, the reactions enabled by the gene are removed from the network and the synthetic accessibility metric is recalculated. An increase in the total number of steps is predicted to cause lethality. Wunderlich and Mirny showed this simple, parameter-free approach predicted knockout lethality in E. coli and S. cerevisiae as well as elementary mode analysis and flux balance analysis in a variety of media.[33]
Applications of a reconstruction
- Several inconsistencies exist between gene, enzyme, and reaction databases and published literature sources regarding the metabolic information of an organism. A reconstruction is a systematic verification and compilation of data from various sources that takes into account all of the discrepancies.
- The combination of relevant metabolic and genomic information of an organism.
- Metabolic comparisons can be performed between various organisms of the same species as well as between different organisms.
- Analysis of synthetic lethality[34]
- Predict adaptive evolution outcomes[35]
- Use in metabolic engineering for high value outputs
Reconstructions and their corresponding models allow the formulation of hypotheses about the presence of certain enzymatic activities and the production of metabolites that can be experimentally tested, complementing the primarily discovery-based approach of traditional microbial biochemistry with hypothesis-driven research.[36] The results these experiments can uncover novel pathways and metabolic activities and decipher between discrepancies in previous experimental data. Information about the chemical reactions of metabolism and the genetic background of various metabolic properties (sequence to structure to function) can be utilized by genetic engineers to modify organisms to produce high value outputs whether those products be medically relevant like pharmaceuticals; high value chemical intermediates such as terpenoids and isoprenoids; or biotechnological outputs like biofuels.
Metabolic network reconstructions and models are used to understand how an organism or parasite functions inside of the host cell. For example, if the parasite serves to compromise the immune system by lysing macrophages, then the goal of metabolic reconstruction/simulation would be to determine the metabolites that are essential to the organism's proliferation inside of macrophages. If the proliferation cycle is inhibited, then the parasite would not continue to evade the host's immune system. A reconstruction model serves as a first step to deciphering the complicated mechanisms surrounding disease. These models can also look at the minimal genes necessary for a cell to maintain virulence. The next step would be to use the predictions and postulates generated from a reconstruction model and apply it to discover novel biological functions such as drug-engineering and drug delivery techniques.
See also
- Metabolic network
- Computer simulation
- Computational systems biology
- Metabolic pathway
- Metagenomics
- Metabolic control analysis
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Franke; Siezen, Teusink (2005). "Reconstructing the metabolic network of a bacterium from its genome.". Trends in Microbiology 13 (11): 550–558. doi:10.1016/j.tim.2005.09.001. PMID 16169729.
- ↑ 2.0 2.1 2.2 Thiele, Ines; Bernhard Ø Palsson (January 2010). "A protocol for generating a high-quality genome-scale metabolic reconstruction". Nature Protocols 5 (1): 93–121. doi:10.1038/nprot.2009.203. PMC 3125167. PMID 20057383.
- ↑ 3.0 3.1 Fleischmann, R. D.; Adams, M. D.; White, O; Clayton, R. A.; Kirkness, E. F.; Kerlavage, A. R.; Bult, C. J.; Tomb, J. F.; Dougherty, B. A.; Merrick, J. M. (1995). "Whole-genome random sequencing and assembly of Haemophilus influenzae Rd". Science 269 (1995): 496–512. doi:10.1126/science.7542800. PMID 7542800.
- ↑ The C. elegans Sequencing Consortium (1998). "Genome Sequence of the Nematode C. elegans: A Platform for Investigating Biology". Science 282 (5396): 2012–2018. doi:10.1126/science.282.5396.2012. PMID 9851916.
- ↑ Edwards, J. S. et al. (May 2000). "The Escherichia coli MG1655 in silico metabolic genotype: Its definition, characteristics, and capabilities". PNAS 97 (10): 5528–5533. doi:10.1073/pnas.97.10.5528. PMC 25862. PMID 10805808.
- ↑ Forster, J. et al. (February 2003). "Genome-Scale Reconstruction of the Saccharomyces cerevisiae Metabolic Network". Genome Research 13 (2): 244–253. doi:10.1101/gr.234503. PMC 420374. PMID 12566402. Missing
|last4=in Authors list (help) - ↑ Sheikh, Kashif et al. (January 2005). "Modeling Hybridoma Cell Metabolism Using a Generic Genome-Scale Metabolic Model of Mus musculus". Biotechnology Resources 21 (1): 112–121. doi:10.1021/bp0498138.
- ↑ Romero, Pedro; Jonathan Wagg; Michelle L Green; Dale Kaiser; Markus Krummenacker; Peter D Karp (June 2004). "Computational prediction of human metabolic pathways from the complete human genome". Genome Biology 6 (1): R2. doi:10.1186/gb-2004-6-1-r2. PMID 15642094.
- ↑ Duarte, N. C. et al. (January 2007). "Global reconstruction of the human metabolic network based on genomic and bibliomic data". PNAS 104 (6): 1777–1782. doi:10.1073/pnas.0610772104. PMC 1794290. PMID 17267599.
- ↑ Jamshidi, Neema; B. O. Palsson (June 2007). "Investigating the metabolic capabilities of Mycobacterium tuberculosis H". BMC Systems Biology 1: 26. doi:10.1186/1752-0509-1-26. PMC 1925256. PMID 17555602.
- ↑ Oh, Y.-K. et al. (September 2007). "Genome-scale Reconstruction of Metabolic Network in Bacillus subtilis Based on High-throughput Phenotyping and Gene Essentiality Data". Journal of Biological Chemistry 282 (39): 28791–28799. doi:10.1074/jbc.M703759200. PMID 17573341.
- ↑ Fu, Pengcheng (October 2008). "Genome-scale modeling of Synechocystis sp. PCC 6803 and prediction of pathway insertion". Journal of Chemical Technology and Biotechnology 84 (4): 473–483. doi:10.1002/jctb.2065.
- ↑ Raghunathan, Anu et al. (April 2009). "Constraint-based analysis of metabolic capacity of Salmonella typhimurium during host-pathogen interaction". BMC Systems Biology 3: 38. doi:10.1186/1752-0509-3-38. PMC 2678070. PMID 19356237.
- ↑ de Oliveira Dal'Molin, C. G.; Quek, L.-E.; Palfreyman, R. W.; Brumbley, S. M.; Nielsen, L. K. (February 2010). "AraGEM, a Genome-Scale Reconstruction of the Primary Metabolic Network in Arabidopsis". Plant Physiology 152 (2): 579–589. doi:10.1104/pp.109.148817. PMC 2815881. PMID 20044452.
- ↑ Karp et al. (January 2010). "Pathway Tools version 13.0: Integrated Software for Pathway/Genome Informatics and Systems Biology". Briefings in Bioinformatics 11 (1): 40–79. doi:10.1093/bib/bbp043. PMC 2810111. PMID 19955237.
- ↑ Wrzodek, Clemens; Büchel, Finja; Ruff, Manuel; Dräger, Andreas; Zell, Andreas (2013). "Precise generation of systems biology models from KEGG pathways". BMC Systems Biology 7 (1): 15. doi:10.1186/1752-0509-7-15.
- ↑ Wrzodek, Clemens; Dräger, Andreas; Zell, Andreas (23 June 2011). "KEGGtranslator: visualizing and converting the KEGG PATHWAY database to various formats". Bioinformatics 27 (16): 2314–2315. doi:10.1093/bioinformatics/btr377. PMID 21700675.
- ↑ Chaouiya, Claudine; Bérenguier, Duncan; Keating, Sarah M; Naldi, Aurélien; van Iersel, Martijn P; Rodriguez, Nicolas; Dräger, Andreas; Büchel, Finja; Cokelaer, Thomas; Kowal, Bryan; Wicks, Benjamin; Gonçalves, Emanuel; Dorier, Julien; Page, Michel; Monteiro, Pedro T; von Kamp, Axel; Xenarios, Ioannis; de Jong, Hidde; Hucka, Michael; Klamt, Steffen; Thieffry, Denis; Le Novère, Nicolas; Saez-Rodriguez, Julio; Helikar, Tomáš (2013). "SBML qualitative models: a model representation format and infrastructure to foster interactions between qualitative modelling formalisms and tools". BMC Systems Biology 7 (1): 135. doi:10.1186/1752-0509-7-135.
- ↑ Henry, CS; DeJongh M; Best AA; Frybarger PM; Linsay B; Stevens RL (September 2010). "High-throughput Generation and Optimization of Genome-scale Metabolic Models". Nature Biotechnology 28 (9): 977–982. doi:10.1038/nbt.1672. PMID 20802497.
- ↑ Chindelevitch, Leonid; Sarah Stanley; Deborah Hung; Aviv Regev; Bonnie Berger (January 2012). "MetaMerge: scaling up genome-scale metabolic reconstructions with application to Mycobacterium tuberculosis". Genome Biology 13 (r6): R6. doi:10.1186/gb-2012-13-1-r6.
- ↑ 21.0 21.1 Ivanova, N.; A. Lykidis (2009). "Metabolic Reconstruction". Encyclopedia of Microbiology, 3rd Ed.: 607–621. doi:10.1016/B978-012373944-5.00010-9. ISBN 9780123739445.
- ↑ Papin JA, Stelling J, Price ND, Klamt S, Schuster S, Palsson BO. Comparison of network-based pathway analysis methods. Trends Biotechnol. 2004 Aug;22(8) 400-5.
- ↑ Lewis, N.E., Nagarajan, H., & Palsson, B.Ø. Constraining the metabolic genotype–phenotype relationship using a phylogeny of in silico methods. Nature Reviews Microbiology 10, 291-305 (2012).
- ↑ http://cobramethods.wikidot.com/
- ↑ 25.0 25.1 25.2 25.3 Price, Nathan; Jennifer Reed; Jason Papin; Sharon Wiback; Bernhard O Palsson (November 2003). "Network-based analysis of metabolic regulation in the human red blood cell". Journal of Theoretical Biology 225 (2): 185–194. doi:10.1016/s0022-5193(03)00237-6. PMID 14575652.
- ↑ Papin, Jason; Nathan Price; Bernhard O Palsson (December 2002). "Extreme Pathway Lengths and Reaction Participation in Genome-Scale Metabolic Networks". Genome Research 12 (12): 1889–1900. doi:10.1101/gr.327702. PMC 187577. PMID 12466293.
- ↑ 27.0 27.1 Papin, Jason; Nathan Price; Bernhard O Palsson (August 2004). "Comparison of network-based pathway analysis methods". Trends in Biotechnology 22 (8): 400–405. doi:10.1016/j.tibtech.2004.06.010. PMID 15283984.
- ↑ 28.0 28.1 Schuster, S; Fell DA; Dandekar T (March 2000). "A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks". Nature Biotechnology 18 (3): 326–332. doi:10.1038/73786. PMID 10700151.
- ↑ 29.0 29.1 29.2 Stelling, J; Klamt S; Bettenbrock K; Schuster S; Gilles ED (November 2002). "Metabolic network structure determines key aspects of functionality and regulation.". Nature 420 (6912): 190–193. doi:10.1038/nature01166. PMID 12432396.
- ↑ Larhlimi, A; Bockmayr, A. (2009). "A new constraint-based description of the steady-state flux cone of metabolic networks". Discrete Applied Mathematics 157 (10): 2257–2266. doi:10.1016/j.dam.2008.06.039.
- ↑ Dräger, A; Kronfeld M; Ziller MJ; Supper J; Planatscher H; Magnus JB; Oldiges M; Kohlbacher O; Zell A (January 2009). "Modeling metabolic networks in C. glutamicum: a comparison of rate laws in combination with various parameter optimization strategies". BMC Systems Biology 3 (5): 5. doi:10.1186/1752-0509-3-5. PMC 2661887. PMID 19144170.
- ↑ Dräger, Andreas; Hassis, Nadine; Supper, Jochen; Schröder, Adrian; Zell, Andreas (2008). "SBMLsqueezer: A CellDesigner plug-in to generate kinetic rate equations for biochemical networks". BMC Systems Biology 2 (1): 39. doi:10.1186/1752-0509-2-39.
- ↑ Wunderlich, Z; Leonid Mirny (September 2006). "Using the topology of metabolic networks to predict viability of mutant strains". Biophysical Journal 91 (6): 2304–11. doi:10.1529/biophysj.105.080572. PMID 16782788.
- ↑ Costanzo, M et al. (2010). "The Genetic Landscape of a Cell". Science 327 (5964): 425–431. doi:10.1126/science.1180823. PMID 20093466.
- ↑ Fong, SS; Marciniak JY; Palsson BØ (November 2003). "Description and interpretation of adaptive evolution of Escherichia coli K-12 MG1655 by using a genome-scale in silico metabolic model". Journal of Bacteriology 185 (21): 6400–6408. doi:10.1128/JB.185.21.6400-6408.2003. PMC 219384. PMID 14563875.
- ↑ Ivanova, A; A. Lykidis (2009). "Metabolic Reconstruction". Encyclopedia of Microbiology, 3rd Edition: 607–621. doi:10.1016/B978-012373944-5.00010-9. ISBN 9780123739445.
Further reading
- Overbeek R, Larsen N, Walunas T, D'Souza M, Pusch G, Selkov Jr, Liolios K, Joukov V, Kaznadzey D, Anderson I, Bhattacharyya A, Burd H, Gardner W, Hanke P, Kapatral V, Mikhailova N, Vasieva O, Osterman A, Vonstein V, Fonstein M, Ivanova N, Kyrpides N. (2003) The ERGO genome analysis and discovery system. Nucleic Acids Res. 31(1):164-71
- Whitaker, J.W., Letunic, I., McConkey, G.A. and Westhead, D.R. metaTIGER: a metabolic evolution resource. Nucleic Acids Res. 2009 37: D531-8.
External links
- ERGO
- GeneDB
- KEGG
- PathCase Case Western Reserve University
- BRENDA
- BioCyc and Cyclone - provides an open source Java API to the pathway tool BioCyc to extract Metabolic graphs.
- EcoCyc
- MetaCyc
- SEED
- Model SEED
- ENZYME
- SBRI Bioinformatics Tools and Software
- TIGR
- Pathway Tools
- metaTIGER
- Stanford Genomic Resources
- Pathway Hunter Tool
- IMG The Integrated Microbial Genomes system, for genome analysis by the DOE-JGI.
- Systems Analysis, Modelling and Prediction Group at the University of Oxford, Biochemical reaction pathway inference techniques.
- EFMtool provided by Marco Terzer
- SBMLsqueezer
- Cellnet analyzer from Klamt and von Kamp
- Copasi
| ||||||||||||||||||