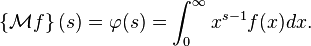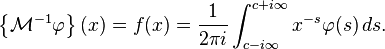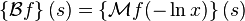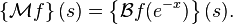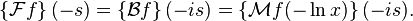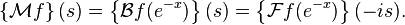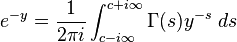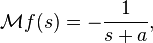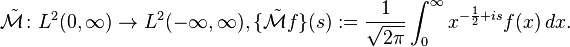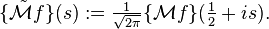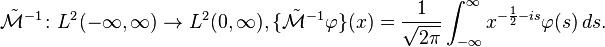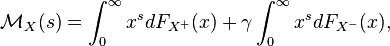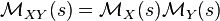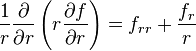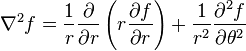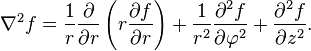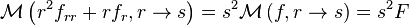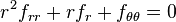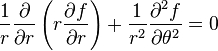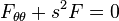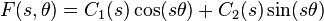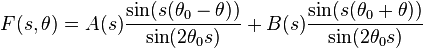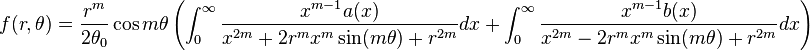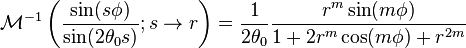Mellin transform

In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform. This integral transform is closely connected to the theory of Dirichlet series, and is often used in number theory, mathematical statistics, and the theory of asymptotic expansions; it is closely related to the Laplace transform and the Fourier transform, and the theory of the gamma function and allied special functions.

The Mellin transform of a function f is

\left\{\mathcal{M}f\right\}(s) = \varphi(s)=\int_0^{\infty} x^{s-1} f(x)dx.

The inverse transform is

\left\{\mathcal{M}^{-1}\varphi\right\}(x) = f(x)=\frac{1}{2 \pi i} \int_{c-i \infty}^{c+i \infty} x^{-s} \varphi(s)\, ds.

The notation implies this is a line integral taken over a vertical line in the complex plane. Conditions under which this inversion is valid are given in the Mellin inversion theorem.

The transform is named after the Finnish mathematician Hjalmar Mellin.

Relationship to other transforms

The two-sided Laplace transform may be defined in terms of the Mellin transform by

\left\{\mathcal{B} f\right\}(s) = \left\{\mathcal{M} f(-\ln x) \right\}(s)

and conversely we can get the Mellin transform from the two-sided Laplace transform by

\left\{\mathcal{M} f\right\}(s) = \left\{\mathcal{B} f(e^{-x})\right\}(s).

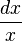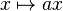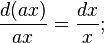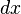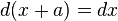The Mellin transform may be thought of as integrating using a kernel xs with respect to the multiplicative Haar measure, \frac{dx}{x}, which is invariant under dilation x \mapsto ax, so that \frac{d(ax)}{ax} = \frac{dx}{x}; the two-sided Laplace transform integrates with respect to the additive Haar measure dx, which is translation invariant, so that d(x+a) = dx.

We also may define the Fourier transform in terms of the Mellin transform and vice versa; if we define the two-sided Laplace transform as above, then

\left\{\mathcal{F} f\right\}(-s) = \left\{\mathcal{B} f\right\}(-is) = \left\{\mathcal{M} f(-\ln x)\right\}(-is).

We may also reverse the process and obtain

\left\{\mathcal{M} f\right\}(s) = \left\{\mathcal{B} f(e^{-x})\right\}(s) = \left\{\mathcal{F} f(e^{-x})\right\}(-is).

The Mellin transform also connects the Newton series or binomial transform together with the Poisson generating function, by means of the Poisson–Mellin–Newton cycle.

Examples

Cahen–Mellin integral

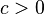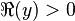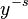For c>0, \Re(y)>0 and y^{-s} on the principal branch, one has

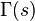e^{-y}= \frac{1}{2\pi i} \int_{c-i\infty}^{c+i\infty} \Gamma(s) y^{-s}\;ds

where \Gamma(s) is the gamma function. This integral is known as the Cahen-Mellin integral.[1]

Number theory

An important application in number theory includes the simple function 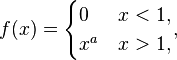f(x)=\begin{cases} 0 & x < 1, \\ x^{a} & x > 1, \end{cases}, for which

\mathcal M f (s)= - \frac 1 {s+a},

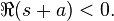
assuming \Re (s+a)<0.

As a unitary operator on L2

In the study of Hilbert spaces, the Mellin transform is often posed in a slightly different way. For functions in 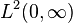L^2(0,\infty) (see Lp space) the fundamental strip always includes 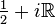\tfrac{1}{2}+i\mathbb{R}, so we may define a linear operator 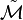\tilde{\mathcal{M}} as

\tilde{\mathcal{M}}\colon L^2(0,\infty)\to L^2(-\infty,\infty), \{\tilde{\mathcal{M}}f\}(s) := \frac{1}{\sqrt{2\pi}}\int_0^{\infty} x^{-\frac{1}{2}+is} f(x)\,dx.

In other words we have set

\{\tilde{\mathcal{M}}f\}(s):=\tfrac{1}{\sqrt{2\pi}}\{\mathcal{M}f\}(\tfrac{1}{2}+is).

This operator is usually denoted by just plain 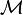\mathcal{M} and called the "Mellin transform", but 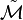\tilde{\mathcal{M}} is used here to distinguish from the definition used elsewhere in this article. The Mellin inversion theorem then shows that 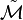\tilde{\mathcal{M}} is invertible with inverse

\tilde{\mathcal{M}}^{-1}\colon L^2(-\infty,\infty) \to L^2(0,\infty), \{\tilde{\mathcal{M}}^{-1}\varphi\}(x) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} x^{-\frac{1}{2}-is} \varphi(s)\,ds.

Furthermore this operator is an isometry, that is to say 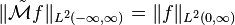\|\tilde{\mathcal{M}} f\|_{L^2(-\infty,\infty)}=\|f\|_{L^2(0,\infty)} for all 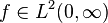f\in L^2(0,\infty) (this explains why the factor of 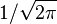1/\sqrt{2\pi} was used). Thus 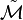\tilde{\mathcal{M}} is a unitary operator.

In probability theory

In probability theory, the Mellin transform is an essential tool in studying the distributions of products of random variables.[2] If X is a random variable, and X+ = max{X,0} denotes its positive part, while X − = max{−X,0} is its negative part, then the Mellin transform of X is defined as [3]

\mathcal{M}_X(s) = \int_0^\infty x^s dF_{X^+}(x) + \gamma\int_0^\infty x^s dF_{X^-}(x),

where γ is a formal indeterminate with γ2 = 1. This transform exists for all s in some complex strip D = {s: a ≤ Re(s) ≤ b}, where a ≤ 0 ≤ b.[3]

The Mellin transform 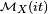\scriptstyle\mathcal{M}_X(it) of a random variable X uniquely determines its distribution function FX.[3] The importance of the Mellin transform in probability theory lies in the fact that if X and Y are two independent random variables, then the Mellin transform of their products is equal to the product of the Mellin transforms of X and Y:[4]

\mathcal{M}_{XY}(s) = \mathcal{M}_X(s)\mathcal{M}_Y(s)

In cylindrical problems with laplacian

In the Laplacian in cylindrical coordinates in a generic dimension (orthogonal coordinates with one angle and one radius, and the remaining lengths) there is always a term:

{1 \over r} {\partial \over \partial r} \left( r {\partial f \over \partial r} \right) = f_{rr} + {f_r \over r}

For example in 2-D polar coordinates the laplacian is:

\nabla^2 f = {1 \over r} {\partial \over \partial r} \left( r {\partial f \over \partial r} \right) + {1 \over r^2} {\partial^2 f \over \partial \theta^2}

and in 3-D cylindrical coordinates the laplacian is,

\nabla^2 f = {1 \over r} {\partial \over \partial r} \left(r {\partial f \over \partial r} \right) + {1 \over r^2} {\partial^2 f \over \partial \varphi^2} + {\partial^2 f \over \partial z^2 }.

This term can be easily treated with the Mellin transform,[5] since:

\mathcal M \left(r^2 f_{rr} + r f_r, r \rightarrow s \right) = s^2 \mathcal M \left(f, r \rightarrow s \right) = s^2 F

For example the 2-D Laplace equation in polar coordinates is the PDE in two variables:

r^2 f_{rr} + r f_r + f_{\theta \theta} = 0

and by multiplication:

{1 \over r} {\partial \over \partial r} \left( r {\partial f \over \partial r} \right) + {1 \over r^2} {\partial^2 f \over \partial \theta^2} = 0

with a Mellin transform on radius becomes the simple harmonic oscillator:

F_{\theta \theta} + s^2 F = 0

with general solution:

F (s, \theta) = C_1(s) \cos (s\theta) + C_2(s) \sin (s \theta)

Now let's impose for example some simple wedge boundary conditions to the original Laplace equation:

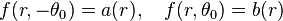
f(r,-\theta_0) = a(r), \quad f(r,\theta_0) = b(r)

these are particularly simple for Mellin transform, becoming:

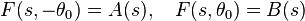F(s,-\theta_0) = A(s), \quad F(s,\theta_0) = B(s) .

These conditions imposed to the solution particularise it to:

F (s, \theta) = A(s) \frac {\sin(s (\theta_0 - \theta))}{\sin (2 \theta_0 s)}+ B(s) \frac {\sin(s (\theta_0 + \theta))}{\sin (2 \theta_0 s)}

Now by the convolution theorem for Mellin transform, the solution in the Mellin domain can be inverted:

f (r, \theta) = \frac{r^m}{2 \theta_0} \cos m \theta \left( \int_0^\infty\frac{ x^{m-1} a(x)}{x^{2m} + 2 r^m x^m \sin(m \theta) + r^{2m}}dx + \int_0^\infty\frac{ x^{m-1} b(x)}{x^{2m} - 2 r^m x^m \sin(m \theta) + r^{2m}}dx \right)

where the following inverse transform relation was employed:

\mathcal M^{-1} \left( \frac {\sin (s \phi)}{\sin (2 \theta_0 s)}; s \rightarrow r \right) = \frac 1 {2 \theta_0} \frac{r^m \sin (m \phi)}{1+2r^m \cos(m \phi) + r^{2m}}

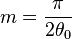where m= \frac \pi {2 \theta_0}.

Applications

The Mellin Transform is widely used in computer science for the analysis of algorithms because of its scale invariance property. The magnitude of the Mellin Transform of a scaled function is identical to the magnitude of the original function. This scale invariance property is analogous to the Fourier Transform's shift invariance property. The magnitude of a Fourier transform of a time-shifted function is identical to the magnitude of the Fourier transform of the original function.

This property is useful in image recognition. An image of an object is easily scaled when the object is moved towards or away from the camera.

Examples

See also

Notes

  1. ↑ Hardy, G. H.; Littlewood, J. E. (1916). "Contributions to the Theory of the Riemann Zeta-Function and the Theory of the Distribution of Primes". Acta Mathematica 41 (1): 119–196. doi:10.1007/BF02422942. (See notes therein for further references to Cahen's and Mellin's work, including Cahen's thesis.)
  2. ↑ Galambos & Simonelli (2004, p. 15)
  3. ↑ 3.0 3.1 3.2 Galambos & Simonelli (2004, p. 16)
  4. ↑ Galambos & Simonelli (2004, p. 23)
  5. ↑ Bhimsen, Shivamoggi, Chapter 6: The Mellin Transform, par. 4.3: Distribution of a Potential in a Wedge, p. 267-8

References

External links