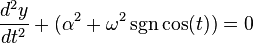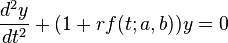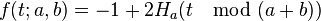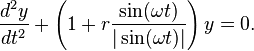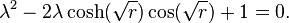Meissner equation

The Meissner equation is a linear ordinary differential equation that is a special case of Hill's equation with the periodic function given as a square wave.^[1] ^[2] There are many ways to write the Meissner equation. One is as

\frac{d^2y}{dt^2} + (\alpha^2 + \omega^2 \sgn \cos(t)) = 0

\frac{d^2y}{dt^2} + ( 1 + r f(t;a,b) ) y = 0

where

f(t;a,b) = -1 + 2 H_a( t \mod (a+b) )

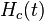and $H_c(t)$ is the Heaviside function shifted to $c$ . Another version is

\frac{d^2y}{dt^2} + \left( 1 + r \frac{\sin( \omega t)}{|\sin(\omega t)|} \right) y = 0.

The Meissner equation was first studied as a toy problem for certain resonance problems. It is also useful for understand resonance problems in evolutionary biology.

Because the time-dependence is piecewise linear, many calculations can be performed exactly, unlike for the Mathieu equation. When 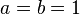$a = b = 1$ , the Floquet exponents are roots of the quadratic equation

\lambda^2 - 2 \lambda \cosh(\sqrt{r}) \cos(\sqrt{r}) + 1 = 0 .

The determinant of the Floquet matrix is 1, implying that origin is a center if 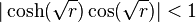$|\cosh(\sqrt{r}) \cos(\sqrt{r})| < 1$ and a saddle node otherwise.

References

↑ Richards, J. A. (1983). Analysis of periodically time-varying systems. Springer-Verlag. ISBN 9783540116899. LCCN 82005978.
↑ E. Meissner (1918). "Ueber Schüttelerscheinungen in Systemen mit periodisch veränderlicher Elastizität". Schweiz. Bauzeit. 72 (11). pp. 95–98.