Mediated reference theory
The mediated reference theory is a semantic theory that posits that words refer to something in the external world, but insists that there is more to the meaning of a name than simply the object to which it refers. It thus stands opposed to the theory of direct reference. Its most famous advocate is the mathematician and philosopher Gottlob Frege. The view was very widely held in the middle of the twentieth century by such philosophers as Sir Peter Strawson and John Searle.
Gottlob Frege
Frege argued that the semantics of words and expressions should be divided into two elements: a sense, which is a "mode of presentation" of the reference of the name; and the reference itself, which is the object to which the name refers. And crucially, for Frege, names that refer to the same object can have different senses. (The difference in "cognitive significance" of 'a = a', and 'a = b', where 'a' and 'b' refer to the same object, has been called Frege's problem or puzzle. Frege introduces the concept of Sinn, or sense, to explain the difference.) For example, "the morning star" and "the evening star" both refer to the object Venus, but they present it to us in different ways: the former as the brightest celestial body visible in the morning, the latter as the brightest celestial body visible in the evening. And so it is, says Frege, that the statement that the morning star is the evening star is potentially informative: its meaning is not just that some object is the same as itself, but (roughly) that the brightest celestial body visible in the morning is the same object as the brightest celestial body visible in the evening.
It is because Frege uses definite descriptions in many of his examples that he is often taken to have endorsed the descriptivist theory of names, an attribution made by Saul Kripke. Most scholars of Frege's work now agree, however, that the attribution is mistaken. If so, then it is important to distinguish the mediated reference theory from the description theory of names.
Bertrand Russell

A paradigm example of an indirect theory of reference is that of philosopher Bertrand Russell. In his direct reference theory, Russell first distinguished between a "logical subject" and a "grammatical subject." The former is the thing in the real world - the referent; while the latter is a description or concept. He then claimed that in logic a "feeling for reality" had to be maintained in order to save discussion from a whole host of troubles. And since the logical subject was made up only of reference, tied together in strings by propositional functions, in logic there was no meaning except reference.
Russell was also quite alive to the topic of descriptions. His particular interest was in "definite and indefinite descriptions." Definite descriptions have the form of "the such-and-such", and indefinite descriptions have the form of "a such-and-such". Russell then made a surprising argument: that "descriptions had meaning only if they were put into bigger statement(s)." This is because his method of translating sentences necessitated that they be rewritten in logical notation, and an isolated description cannot be effectively captured by any such notation.
Take the sentence, "The king of France is bald", for instance. For Russell, what it really translates as (in a reformed, better English) is:
There is at least one x such that: x and nothing else is a King of France, and x is bald.
In this newer, better form, the word "the" no longer appears; it is diffused throughout the rest of the logical translation. This, for Russell, is why the definite description "the king of France" is not meaningful on its own; the word, 'the', doesn't work unless it appears in the context of a full sentence.
Furthermore, the above can be expressed in a more strict logical form (where K(x) means "x is the king of France", B(x) means "x is bald", the bullet means "and", and the arrow means "if-then"):
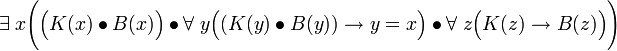 |
Which says: "there is an x such that: x is bald and x is a king of France; and for every y that is a king of France, x is y; and every z that is a king of France is bald". This is a very long way of stating that something is uniquely both king of France and bald.
For Russell, this logical form would provide the speaker of a language with metaphysical insight as to what they are actually speaking about.