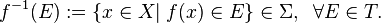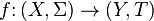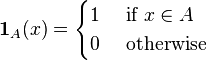Measurable function

A function is Lebesgue measurable if and only if the preimage of each of the sets

[a,\infty]

is a Lebesgue measurable set.

In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration. Specifically, a function between measurable spaces is said to be measurable if the preimage of each measurable set is measurable, analogous to the situation of continuous functions between topological spaces.

In probability theory, the sigma algebra often represents the set of available information, and a function (in this context a random variable) is measurable if and only if it represents an outcome that is knowable based on the available information. In contrast, functions that are not Lebesgue measurable are generally considered pathological, at least in the field of analysis.

Formal definition

Let (X, Σ) and (Y, Τ) be measurable spaces, meaning that X and Y are sets equipped with respective sigma algebras Σ and Τ. A function f: X → Y is said to be measurable if the preimage of E under f is in Σ for every E ∈ Τ; i.e.

f^{-1}(E) := \{ x\in X |\; f(x) \in E \} \in \Sigma,\;\; \forall E \in T.

The notion of measurability depends on the sigma algebras Σ and Τ. To emphasize this dependency, if f: X → Y is a measurable function, we will write

f \colon (X, \Sigma ) \rightarrow ( Y, T )

Caveat

This definition can be deceptively simple, however, as special care must be taken regarding the σ-algebras involved. In particular, when a function f: R → R is said to be Lebesgue measurable what is actually meant is that 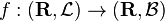$f : (\mathbf{R}, \mathcal{L}) \to (\mathbf{R}, \mathcal{B})$ is a measurable function—that is, the domain and range represent different σ-algebras on the same underlying set (here 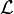$\mathcal{L}$ is the sigma algebra of Lebesgue measurable sets, and 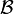$\mathcal{B}$ is the Borel algebra on R). As a result, the composition of Lebesgue-measurable functions need not be Lebesgue-measurable.

By convention a topological space is assumed to be equipped with the Borel algebra generated by its open subsets unless otherwise specified. Most commonly this space will be the real or complex numbers. For instance, a real-valued measurable function is a function for which the preimage of each Borel set is measurable. A complex-valued measurable function is defined analogously. In practice, some authors use measurable functions to refer only to real-valued measurable functions with respect to the Borel algebra.^[1] If the values of the function lie in an infinite-dimensional vector space instead of R or C, usually other definitions of measurability are used, such as weak measurability and Bochner measurability.

Special measurable functions

If (X, Σ) and (Y, Τ) are Borel spaces, a measurable function f: (X, Σ) → (Y, Τ) is also called a Borel function. Continuous functions are Borel functions but not all Borel functions are continuous. However, a measurable function is nearly a continuous function; see Luzin's theorem. If a Borel function happens to be a section of some map 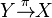$Y\stackrel{\pi}{\to} X$ , it is called a Borel section.

A Lebesgue measurable function is a measurable function 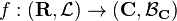$f : (\mathbf{R}, \mathcal{L}) \to (\mathbf{C}, \mathcal{B}_\mathbf{C})$ , where 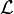$\mathcal{L}$ is the sigma algebra of Lebesgue measurable sets, and 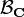$\mathcal{B}_\mathbf{C}$ is the Borel algebra on the complex numbers C. Lebesgue measurable functions are of interest in mathematical analysis because they can be integrated. In the case 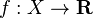$f:X\to\mathbf{R}$ , $f$ is Lebesgue measurable iff 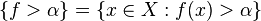$\{f>\alpha\}=\{x\in X:f(x)>\alpha\}$ is measurable for all real $\alpha$ . 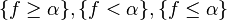This is also equivalent to any of $\{f\ge\alpha\},\{f<\alpha\},\{f\le\alpha\}$ being measurable for all $\alpha$ . 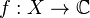Continuous functions, monotone functions, step functions, semicontinuous functions, Riemann-integrable functions, and functions of bounded variation are all Lebesgue measurable.^[2] A function $f:X\to\mathbb{C}$ is measurable iff the real and imaginary parts are measurable.

Random variables are by definition measurable functions defined on sample spaces.

Properties of measurable functions

The sum and product of two complex-valued measurable functions are measurable.^[3] So is the quotient, so long as there is no division by zero.^[1]

The composition of measurable functions is measurable; i.e., if f: (X, Σ₁) → (Y, Σ₂) and g: (Y, Σ₂) → (Z, Σ₃) are measurable functions, then so is g(f(⋅)): (X, Σ₁) → (Z, Σ₃).^[1] But see the caveat regarding Lebesgue-measurable functions in the introduction.

The (pointwise) supremum, infimum, limit superior, and limit inferior of a sequence (viz., countably many) of real-valued measurable functions are all measurable as well.^[1]^[4]

The pointwise limit of a sequence of measurable functions is measurable (if the codomain in endowed with the Borel algebra); note that the corresponding statement for continuous functions requires stronger conditions than pointwise convergence, such as uniform convergence. (This is correct when the counter domain of the elements of the sequence is a metric space. It is false in general; see pages 125 and 126 of.^[5])

Non-measurable functions

Real-valued functions encountered in applications tend to be measurable; however, it is not difficult to find non-measurable functions.

So long as there are non-measurable sets in a measure space, there are non-measurable functions from that space. If (X, Σ) is some measurable space and A ⊂ X is a non-measurable set, i.e. if A ∉ Σ, then the indicator function 1_A: (X, Σ) → R is non-measurable (where R is equipped with the Borel algebra as usual), since the preimage of the measurable set {1} is the non-measurable set A. Here 1_A is given by

\mathbf{1}_A(x) = \begin{cases} 1 & \text{ if } x \in A \\ 0 & \text{ otherwise} \end{cases}

Any non-constant function can be made non-measurable by equipping the domain and range with appropriate σ-algebras. If f: X → R is an arbitrary non-constant, real-valued function, then f is non-measurable if X is equipped with the indiscrete algebra Σ = {∅, X}, since the preimage of any point in the range is some proper, nonempty subset of X, and therefore does not lie in Σ.

Notes

↑ 1.0 1.1 1.2 1.3 Strichartz, Robert (2000). The Way of Analysis. Jones and Bartlett. ISBN 0-7637-1497-6.
↑ Carothers, N. L. (2000). Real Analysis. Cambridge University Press. ISBN 0-521-49756-6.
↑ Folland, Gerald B. (1999). Real Analysis: Modern Techniques and their Applications. Wiley. ISBN 0-471-31716-0.
↑ Royden, H. L. (1988). Real Analysis. Prentice Hall. ISBN 0-02-404151-3.
↑ Dudley, R. M. (2002). Real Analysis and Probability (2 ed.). Cambridge University Press. ISBN 0-521-00754-2.