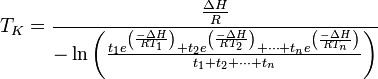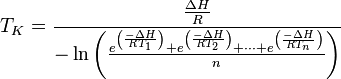Mean kinetic temperature

Mean kinetic temperature (MKT) is a simplified way of expressing the overall effect of temperature fluctuations during storage or transit of perishable goods. The MKT is widely used in the pharmaceutical industry.

The mean kinetic temperature can be expressed as:

T_K=\cfrac{\frac{\Delta H}{R}}{-\ln \left ( \frac{{t_1}e^ \left ( \frac{-\Delta H}{RT_1}\right ) + {t_2}e^ \left ( \frac{-\Delta H}{RT_2}\right ) + \cdots + {t_n}e^ \left ( \frac{-\Delta H}{RT_n}\right )}{{t_1} + {t_2} + \cdots + {t_n}} \right )}

Where:

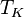T_K\,\! is the mean kinetic temperature in kelvins
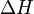\Delta H\,\! is the activation energy (typically within 60–100 kJ·mol−1 for solids or liquids)
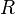R\,\! is the gas constant
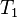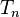T_1\,\! to T_n\,\! are the temperatures at each of the sample points in kelvins
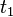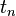t_1\,\! to t_n\,\! are time intervals at each of the sample points


When the temperature readings are taken at the same interval (i.e., 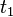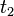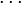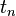t_1\,\! = t_2\,\! = \cdots = t_n\,\!), the above equation is reduced to:

T_K=\cfrac{\frac{\Delta H}{R}}{-\ln \left ( \frac{e^ \left ( \frac{-\Delta H}{RT_1}\right ) + e^ \left ( \frac{-\Delta H}{RT_2}\right ) + \cdots + e^ \left ( \frac{-\Delta H}{RT_n}\right )}{n} \right )}

Where:

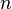n\,\! is the number of temperature sample points


As the activation energy approaches zero, the MKT approaches the harmonic mean temperature. As the activation energy approaches infinity, the MKT approaches the maximum of the temperature sample points.

External links

Wikimedia Commons has media related to Mean kinetic temperature.