Mazur manifold
In differential topology, a branch of mathematics, a Mazur manifold is a contractible, compact, smooth 4-dimensional manifold (with boundary) which is not diffeomorphic to the standard 4-ball. The boundary of a Mazur manifold is necessarily a homology 3-sphere.
Frequently the term Mazur manifold is restricted to a special class of the above definition: 4-manifolds that have a handle decomposition containing exactly three handles: a single 0-handle, a single 1-handle and single 2-handle. This is equivalent to saying the manifold must be of the form 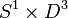 union a 2-handle. An observation of Mazur's shows that the double of such manifolds is diffeomorphic to
union a 2-handle. An observation of Mazur's shows that the double of such manifolds is diffeomorphic to 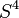 with the standard smooth structure.
with the standard smooth structure.
Some properties
In general the double of a Mazur manifold is a homotopy 4-sphere, thus such manifolds are a source of possible counter-examples to the smooth Poincaré conjecture in dimension 4.
History
Barry Mazur[1] and Valentin Poenaru[2] discovered these manifolds simultaneously. Akbulut and Kirby showed that the Brieskorn homology spheres 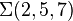 ,
, 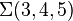 and
and 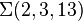 are boundaries of Mazur manifolds.[3] This results were later generalized to other contractible manifolds by Casson, Harer and Stern.[4][5][6] One of the Mazur manifolds is also an example of an Akbulut cork[7] which can be used to construct exotic 4-manifolds.[8]
are boundaries of Mazur manifolds.[3] This results were later generalized to other contractible manifolds by Casson, Harer and Stern.[4][5][6] One of the Mazur manifolds is also an example of an Akbulut cork[7] which can be used to construct exotic 4-manifolds.[8]
Mazur manifolds have been used by Fintushel and Stern[9] to construct exotic actions of a group of order 2 on the 4-sphere.
Mazur's discovery was surprising for several reasons:
- Every smooth homology sphere in dimension
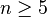 is homeomorphic to the boundary of a compact contractible smooth manifold. This follows from the work of Kervaire[10] and the h-cobordism theorem. Slightly more strongly, every smooth homology 4-sphere is diffeomorphic to the boundary of a compact contractible smooth 5-manifold (also by the work of Kervaire). But not every homology 3-sphere is diffeomorphic to the boundary of a contractible compact smooth 4-manifold. For example, the Poincaré homology sphere does not bound such a 4-manifold because the Rochlin invariant provides an obstruction.
is homeomorphic to the boundary of a compact contractible smooth manifold. This follows from the work of Kervaire[10] and the h-cobordism theorem. Slightly more strongly, every smooth homology 4-sphere is diffeomorphic to the boundary of a compact contractible smooth 5-manifold (also by the work of Kervaire). But not every homology 3-sphere is diffeomorphic to the boundary of a contractible compact smooth 4-manifold. For example, the Poincaré homology sphere does not bound such a 4-manifold because the Rochlin invariant provides an obstruction.
- Every smooth homology sphere in dimension
- The H-cobordism Theorem implies that, at least in dimensions
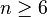 there is a unique contractible
there is a unique contractible  -manifold with simply-connected boundary, where uniqueness is up to diffeomorphism. This manifold is the unit ball
-manifold with simply-connected boundary, where uniqueness is up to diffeomorphism. This manifold is the unit ball 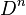 . It's an open problem as to whether or not
. It's an open problem as to whether or not 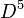 admits an exotic smooth structure, but by the h-cobordism theorem, such an exotic smooth structure, if it exists, must restrict to an exotic smooth structure on
admits an exotic smooth structure, but by the h-cobordism theorem, such an exotic smooth structure, if it exists, must restrict to an exotic smooth structure on 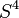 . Whether or not
. Whether or not 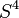 admits an exotic smooth structure is equivalent to another open problem, the smooth Poincaré conjecture in dimension four. Whether or not
admits an exotic smooth structure is equivalent to another open problem, the smooth Poincaré conjecture in dimension four. Whether or not 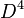 admits an exotic smooth structure is another open problem, closely linked to the Schoenflies problem in dimension four.
admits an exotic smooth structure is another open problem, closely linked to the Schoenflies problem in dimension four.
- The H-cobordism Theorem implies that, at least in dimensions
Mazur's Observation
Let  be a Mazur manifold that is constructed as
be a Mazur manifold that is constructed as 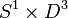 union a 2-handle. Here is a sketch of Mazur's argument that the double of such a Mazur manifold is
union a 2-handle. Here is a sketch of Mazur's argument that the double of such a Mazur manifold is 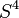 .
. ![M \times [0,1]](../I/m/8133e1a3347bba0eb3f5fa606d7e548f.png) is a contractible 5-manifold constructed as
is a contractible 5-manifold constructed as 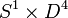 union a 2-handle. The 2-handle can be unknotted since the attaching map is a framed knot in the 4-manifold
union a 2-handle. The 2-handle can be unknotted since the attaching map is a framed knot in the 4-manifold 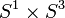 . So
. So 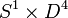 union the 2-handle is diffeomorphic to
union the 2-handle is diffeomorphic to 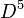 . The boundary of
. The boundary of 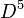 is
is 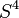 . But the boundary of
. But the boundary of ![M \times [0,1]](../I/m/8133e1a3347bba0eb3f5fa606d7e548f.png) is the double of
is the double of  .
.
References
- ↑ Mazur, Barry A note on some contractible $4$-manifolds. Ann. of Math. (2) 73 1961 221--228.
- ↑ Valentin Poenaru, Les decompositions de l'hypercube en produit topologique, Bull. Soc. Math. France 88 (1960), 113-129.
- ↑ S.Akbulut, R.Kirby, "Mazur manifolds," Michigan Math. J. 26 (1979), 259--284.
- ↑ A.Casson, J.Harer, "Some homology lens spaces which bound rational homology balls." Pacific. J. Math. Vol 96, No 1, (1981) 23–36.
- ↑ H.Fickle, "Knots, Z-Homology 3-spheres and contractible 4-manifolds," pp. 467--493, Houston J. Math. Vol 10, No. 4 (1984).
- ↑ R.Stern,"Some Brieskorn spheres which bound contractible manifolds," Notices Amer. Math. Soc 25 (1978), A448.
- ↑ Akbulut cork
- ↑ S.Akbulut, "A Fake compact contractible 4-manifold" , Journ. of Diff. Geom. 33, (1991), 335-356
- ↑ Fintushel, Ronald; Stern, Ronald J. An exotic free involution on $S^{4}$. Ann. of Math. (2) 113 (1981), no. 2, 357--365.
- ↑ Kervaire, Michel A. Smooth homology spheres and their fundamental groups. Trans. Amer. Math. Soc. 144 1969 67--72.