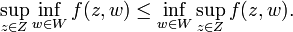Max–min inequality

In mathematics, the max–min inequality is as follows: for any function 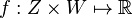$f: Z \times W \mapsto \mathbb{R}$

\sup_{z \in Z} \inf_{w \in W} f(z, w) \leq \inf_{w \in W} \sup_{z \in Z} f(z, w). \,

When equality holds one says that 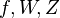$f, W, Z$ satisfies the strong max–min property (or the saddle-point property).

Proof

Define 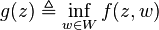$g(z) \triangleq \inf_{w \in W} f(z, w)$ .

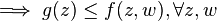
$\implies g(z) \leq f(z, w), \forall z, w$

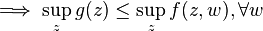
$\implies \sup_z g(z) \leq \sup_z f(z, w) , \forall w$

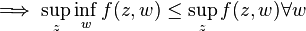
$\implies \sup_z \inf_w f(z,w) \leq \sup_z f(z, w) \forall w$

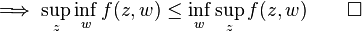
$\implies \sup_z \inf_w f(z,w) \leq \inf_w \sup_z f(z, w) \qquad \square$

Boyd, Stephen; Vandenberghe, Lieven (2004), Convex Optimization, Cambridge University Press

"Max Min of function less than Min max of function", http://math.stackexchange.com/q/186697/61602