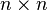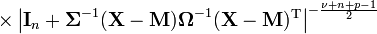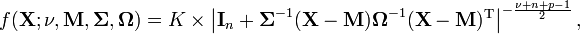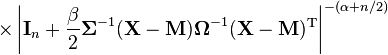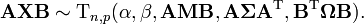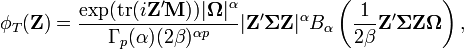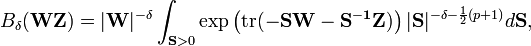Matrix t-distribution
In statistics, the matrix t-distribution (or matrix variate t-distribution) is the generalization of the multivariate t-distribution from vectors to matrices.[1] The matrix t-distribution shares the same relationship with the multivariate t-distribution that the matrix normal distribution shares with the multivariate normal distribution. For example, the matrix t-distribution is the compound distribution that results from sampling from a matrix normal distribution having sampled the covariance matrix of the matrix normal from an inverse Wishart distribution.
In a Bayesian analysis of a multivariate linear regression model based on the matrix normal distribution, the matrix t-distribution is the posterior predictive distribution.
Definition
| Notation |
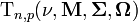 |
|---|---|
| Parameters |
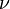 degrees of freedom degrees of freedom |
| Support |
 |
|
| |
| CDF | No analytic expression |
| Mean |
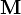 if if  , else undefined , else undefined |
| Mode |
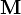 |
| Variance |
 if if 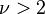 , else undefined , else undefined |
| CF | see below |
For a matrix t-distribution, the probability density function at the point 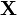 of an
of an 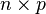 space is
space is
where the constant of integration K is given by
Here 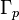 is the multivariate gamma function.
is the multivariate gamma function.
The characteristic function and various other properties can be derived from the generalized matrix t-distribution (see below).
Generalized matrix t-distribution
| Notation |
 |
|---|---|
| Parameters |
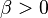 scale parameter scale parameter |
| Support |
 |
|
| |
| CDF | No analytic expression |
| Mean |
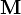 |
| Variance |
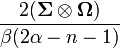 |
| CF | see below |
The generalized matrix t-distribution is a generalization of the matrix t-distribution with two parameters α and β in place of ν.[2]
This reduces to the standard matrix t-distribution with 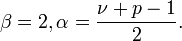
The generalized matrix t-distribution is the compound distribution that results from an infinite mixture of a matrix normal distribution with an inverse multivariate gamma distribution placed over either of its covariance matrices.
Properties
If 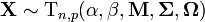 then
then
This makes use of the following:
If 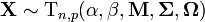 and
and 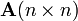 and
and 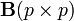 are nonsingular matrices then
are nonsingular matrices then
The characteristic function is[2]
where
and where  is the type-two Bessel function of Herz of a matrix argument.
is the type-two Bessel function of Herz of a matrix argument.
See also
Notes
- ↑ Zhu, Shenghuo and Kai Yu and Yihong Gong (2007). "Predictive Matrix-Variate t Models." In J.C. Platt, D. Koller, Y. Singer, and S. Roweis, editors, NIPS '07: Advances in Neural Information Processing Systems 20, pages 1721-1728. MIT Press, Cambridge, MA, 2008. The notation is changed a bit in this article for consistency with the matrix normal distribution article.
- ↑ 2.0 2.1 Iranmanesh, Anis, M. Arashi and S. M. M. Tabatabaey (2010). "On Conditional Applications of Matrix Variate Normal Distribution". Iranian Journal of Mathematical Sciences and Informatics, 5:2, pp. 33–43.
 scale (
scale (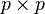
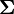 scale (
scale (