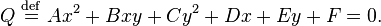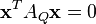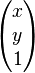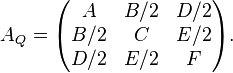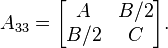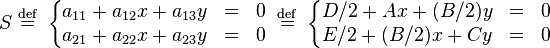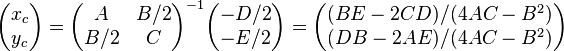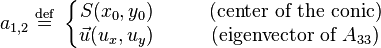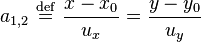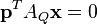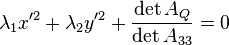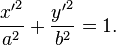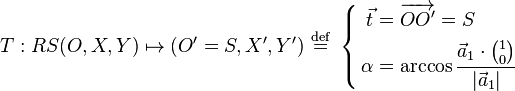Matrix representation of conic sections

In mathematics, the matrix representation of conic sections is one way of studying a conic section, its axis, vertices, foci, tangents, and the relative position of a given point. We can also study conic sections whose axes aren't parallel to our coordinate system.

Conic sections have the form of a second-degree polynomial:

Q \ \stackrel{\mathrm{def}}{=}\ Ax^2+Bxy+Cy^2+Dx+Ey+F=0. \,

That can be written as:

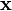\mathbf{x}^T A_Q\mathbf{x}=0

Where $\mathbf{x}$ is the homogeneous coordinate vector:

\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}

And $A_Q$ a matrix:

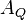A_Q = \begin{pmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{pmatrix}.

Classification

Regular and degenerate conic sections can be distinguished^[1]^:p.63;^[2]^:p.70;^[3]^:pp.101-111 based on the determinant of A_Q.

If 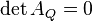$\det A_Q = 0$ , the conic is degenerate.

If Q is not degenerate, we can see what type of conic section it is by computing the minor 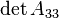$\det A_{33}$ (that is, the determinant of the submatrix resulting from removing the last row and the last column of A_Q):

A_{33} = \begin{bmatrix} A & B/2 \\ B/2 & C \end{bmatrix}.

If and only if 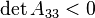$\det A_{33} < 0$ , it is a hyperbola.
If and only if 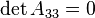$\det A_{33} = 0$ , it is a parabola.
If and only if 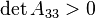$\det A_{33} > 0$ , it is an ellipse.

In the case of an ellipse, we can make a further distinction between an ellipse and a circle by comparing the last two diagonal elements corresponding to x² and y².

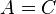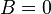If $A = C$ and $B = 0$ , it is a circle.

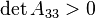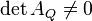Moreover, in the case of a non-degenerate ellipse (with $\det A_{33} > 0$ and $\det A_Q \ne 0$ ), we have a real ellipse if 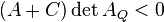$(A + C) \det A_Q < 0$ but an imaginary ellipse if 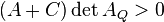$(A + C) \det A_Q > 0$ . An example of the latter is 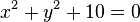$x^2 + y^2 + 10 = 0$ , which has no real-valued solutions.

If the conic section is degenerate (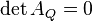 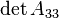$\det A_Q = 0$ ), $\det A_{33}$ still allows us to distinguish its form:

If and only if 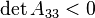$\det A_{33} < 0$ , it is two intersecting lines.
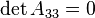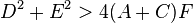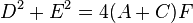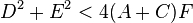If and only if $\det A_{33} = 0$ , it is two parallel straight lines. These lines are distinct and real if $D^2+E^2>4(A+C)F$ , coincident if $D^2+E^2=4(A+C)F$ , and distinct and imaginary if $D^2+E^2<4(A+C)F$ .
If and only if 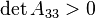$\det A_{33} > 0$ , it is a single point.

Center

In the center of the conic, the gradient of the quadratic form $Q$ vanishes, so: $\nabla Q =[ \frac{\partial Q}{\partial x} , \frac{\partial Q}{\partial y}] = [0,0].$

We can calculate the center by taking the first two rows of the associated matrix 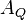$A_Q$ , multiplying each by (x, y, 1)^T, setting both inner products equal to 0, and solving the system.

S \ \stackrel{\mathrm{def}}{=}\ \left\{ \begin{matrix} a_{11} + a_{12}x + a_{13}y & = & 0 \\ a_{21} + a_{22}x + a_{23}y & = & 0 \end{matrix} \right. \ \stackrel{\mathrm{def}}{=}\ \left\{\begin{matrix} D/2 + Ax + (B/2)y & = & 0 \\ E/2 + (B/2)x + Cy & = & 0 \end{matrix} \right.

This becomes

\begin{pmatrix} x_c \\ y_c \end{pmatrix} = \begin{pmatrix} A & B/2 \\ B/2 & C \end{pmatrix}^{-1} \begin{pmatrix} -D/2 \\ -E/2 \end{pmatrix} = \begin{pmatrix} (BE-2CD)/(4AC-B^2) \\ (DB-2AE)/(4AC-B^2) \end{pmatrix}

Note that in the case of a parabola, defined by (4AC-B²) = 0, there is no center since the above denominators become zero.

Axes

The major and minor axes are two lines determined by the center of the conic as a point and eigenvectors of the associated matrix as vectors of direction.

a_{1,2} \ \stackrel{\mathrm{def}}{=}\ \left\{\begin{matrix} S(x_0,y_0) &\qquad \mbox{(center of the conic)}\\ \vec u(u_x,u_y) &\qquad \mbox{(eigenvector of }A_{33}) \end{matrix} \right.

So we can write a canonical equation:

a_{1,2} \ \stackrel{\mathrm{def}}{=}\ \frac{x-x_0}{u_x} = \frac{y-y_0}{u_y}

Because a 2x2 matrix has 2 eigenvectors, we obtain 2 axes.

Vertices

For a general conic we can determine its vertices by calculating the intersection of the conic and its axes — in other words, by solving the system:

V \ \stackrel{\mathrm{def}}{=}\ \left\{\begin{matrix} & e &\qquad \mbox{(axis)} \\ & Q &\qquad \mbox{(the general equation of the conic)} \end{matrix} \right.

Tangents

Through a given point, P, there are generally two lines tangent to a conic. Expressing P as a column vector, p, the two points of tangency are the intersections of the conic with the line whose equation is

\mathbf{p}^T A_Q\mathbf{x}=0

When P is on the conic, the line is the tangent there. When P is inside an ellipse, the line is the set of all points whose own associated line passes through P. This line is called the polar of the pole P with respect to the conic.

Just as P uniquely determines its polar line (with respect to a given conic), so each line determines a unique P. This is thus an expression of geometric duality between points and lines in the plane.

As special cases, the center of a conic is the pole of the line at infinity, and each asymptote of a hyperbola is a polar (a tangent) to one of its points at infinity.

Using the theory of poles and polars, the problem of finding the four mutual tangents of two conics reduces to finding the intersection of two conics.

Reduced equation

The reduced equation of a conic section is the equation of a conic section translated and rotated so that its center lies in the center of the coordinate system and its axes are parallel to the coordinate axes. This is equivalent to saying that the coordinates are moved to satisfy these properties. See the figure.

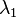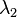If $\lambda_1$ and $\lambda_2$ are the eigenvalues of the matrix A₃₃, the reduced equation can be written as^[4]

\lambda_1 x'^2 + \lambda_2 y'^2 + \frac{\det A_Q}{\det A_{33}} = 0

Dividing by 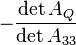$-\frac{\det A_Q}{\det A_{33}}$ we obtain a reduced canonical equation. For example, for an ellipse:

\frac{{x'}^2}{a^2} + \frac{{y'}^2}{b^2} = 1.

From here we get a and b.

The transformation of coordinates is given by:

T: RS(O,X,Y) \mapsto (O'=S,X',Y') \ \stackrel{\mathrm{def}}{=}\ \left\{\begin{align} \vec t &= \overrightarrow {OO'} = S\\ \alpha &= \operatorname{arccos} \frac{\vec a_1 \cdot {1 \choose 0}}{|\vec a_1|} \end{align} \right.

References

↑ Lawrence, J. Dennis, A Catalog of Special Plane Curves, Dover Publ., 1972.
↑ Spain, Barry, Analytical Conics, Dover, 2007.
↑ Pettofrezzo, Anthony, Matrices and Transformations, Dover, 1966.
↑ Ayoub, A. B., "The central conic sections revisited", Mathematics Magazine 66(5), 1993, 322-325.