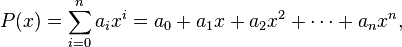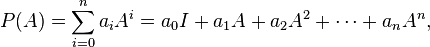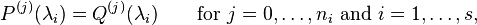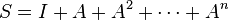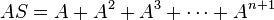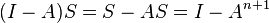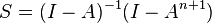Matrix polynomial

Not to be confused with Polynomial matrix.

In mathematics, a matrix polynomial is a polynomial with matrices as variables. Given an ordinary, scalar-valued polynomial

P(x) = \sum_{i=0}^n{ a_i x^i} =a_0 + a_1 x+ a_2 x^2 + \cdots + a_n x^n,

this polynomial evaluated at a matrix A is

P(A) = \sum_{i=0}^n{ a_i A^i} =a_0 I + a_1 A + a_2 A^2 + \cdots + a_n A^n,

where I is the identity matrix.^[1]

A matrix polynomial equation is an equality between two matrix polynomials, which holds for the specific matrices in question. A matrix polynomial identity is a matrix polynomial equation which holds for all matrices A in a specified matrix ring M_n(R).

Characteristic and minimal polynomial

The characteristic polynomial of a matrix A is a scalar-valued polynomial, defined by 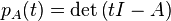$p_A(t) = \det \left(tI - A\right)$ . The Cayley–Hamilton theorem states that if this polynomial is viewed as a matrix polynomial and evaluated at the matrix A itself, the result is the zero matrix: 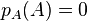$p_A(A) = 0$ . The characteristic polynomial is thus a polynomial which annihilates A.

There is a unique monic polynomial of minimal degree which annihilates A; this polynomial is the minimal polynomial. Any polynomial which annihilates A (such as the characteristic polynomial) is a multiple of the minimal polynomial.^[2]

It follows that that given two polynomials P and Q, we have 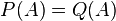$P(A) = Q(A)$ if and only if

P^{(j)}(\lambda_i) = Q^{(j)}(\lambda_i) \qquad \text{for } j = 0,\ldots,n_i \text{ and } i = 1,\ldots,s,

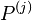where $P^{(j)}$ denotes the jth derivative of P and 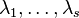$\lambda_1, \dots, \lambda_s$ are the eigenvalues of A with corresponding indices 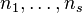$n_1, \dots, n_s$ (the index of an eigenvalue is the size of its largest Jordan block).^[3]

Matrix geometrical series

Matrix polynomials can be used to sum a matrix geometrical series as one would an ordinary geometric series,

S=I+A+A^2+\cdots +A^n

AS=A+A^2+A^3+\cdots +A^{n+1}

(I-A)S=S-AS=I-A^{n+1}

S=(I-A)^{-1}(I-A^{n+1})

If I − A is nonsingular one can evaluate the expression for the sum S.

Notes

References

Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics 58. Lancaster, PA: Society for Industrial and Applied Mathematics. ISBN 0-898716-81-0. Zbl 1170.15300.
Higham, Nicholas J. (2000). Functions of Matrices: Theory and Computation. SIAM. ISBN 089-871-777-9. .
Horn, Roger A.; Johnson, Charles R. (1990). Matrix Analysis. Cambridge University Press. ISBN 978-0-521-38632-6. .

Matrix polynomial

Characteristic and minimal polynomial

Matrix geometrical series

See also

Notes

References