Matrix of ones

In mathematics, a matrix of ones or all-ones matrix is a matrix where every element is equal to one.^[1] Examples of standard notation are given below:

J_2=\begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix};\quad J_3=\begin{pmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{pmatrix};\quad J_{2,5}=\begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \end{pmatrix}.\quad

Some sources call the all-ones matrix the unit matrix,^[2] but that term may also refer to the identity matrix, a different matrix.

Properties

For an n×n matrix of ones J, the following properties hold:

The trace of J is n,^[3] and the determinant is 1 if n is 1, or 0 otherwise.
The rank of J is 1 and the eigenvalues are n (once) and 0 (n-1 times).^[4]
J is positive semi-definite matrix. This follows from the previous property.
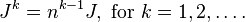$J^k = n^{k-1} J, \mbox{ for } k=1,2,\ldots.\,$ ^[5]
The matrix 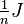$\tfrac1n J$ is idempotent. This is a simple corollary of the above.^[5]
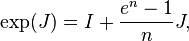$\exp(J) = I + \frac{ e^n-1}{n} J,$ where exp(J) is the matrix exponential.
J is the neutral element of the Hadamard product.^[6]
If A is the adjacency matrix of a n-vertex undirected graph G, and J is the all-ones matrix of the same dimension, then G is a regular graph if and only if AJ = JA.^[7]

References

↑ Horn, Roger A.; Johnson, Charles R. (2012), "0.2.8 The all-ones matrix and vector", Matrix Analysis, Cambridge University Press, p. 8, ISBN 9780521839402 .
↑ Weisstein, Eric W., "Unit Matrix", MathWorld.
↑ Stanley, Richard P. (2013), Algebraic Combinatorics: Walks, Trees, Tableaux, and More, Springer, Lemma 1.4, p. 4, ISBN 9781461469988 .
↑ Stanley (2013); Horn & Johnson (2012), p. 65.
↑ 5.0 5.1 Timm, Neil H. (2002), Applied Multivariate Analysis, Springer texts in statistics, Springer, p. 30, ISBN 9780387227719 .
↑ Smith, Jonathan D. H. (2011), Introduction to Abstract Algebra, CRC Press, p. 77, ISBN 9781420063721 .
↑ Godsil, Chris (1993), Algebraic Combinatorics, CRC Press, Lemma 4.1, p. 25, ISBN 9780412041310 .