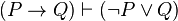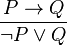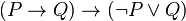Material implication (rule of inference)

Not to be confused with material inference.

Transformation rules
Propositional calculus
Rules of inference
Modus ponens / Modus tollens Biconditional introduction / elimination Conjunction introduction / elimination Disjunction introduction / elimination Disjunctive / Hypothetical syllogism Constructive / Destructive dilemma Absorption Modus ponendo tollens
Rules of replacement
Associativity Commutativity Distributivity Double negation De Morgan's laws Transposition Material implication Exportation Tautology Negation introduction
Predicate logic
Universal generalization / instantiation Existential generalization / instantiation

In propositional logic, material implication ^[1]^[2] is a valid rule of replacement that allows for a conditional statement to be replaced by a disjunction if and only if the antecedent is negated. The rule states that P implies Q is logically equivalent to not-P or Q and can replace each other in logical proofs.

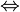P \to Q \Leftrightarrow \neg P \or Q

Where " $\Leftrightarrow$ " is a metalogical symbol representing "can be replaced in a proof with."

Formal notation

The material implication rule may be written in sequent notation:

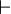(P \to Q) \vdash (\neg P \or Q)

where $\vdash$ is a metalogical symbol meaning that 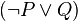$(\neg P \or Q)$ is a syntactic consequence of $(P \to Q)$ in some logical system;

or in rule form:

\frac{P \to Q}{\neg P \or Q}

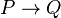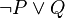where the rule is that wherever an instance of " $P \to Q$ " appears on a line of a proof, it can be replaced with " $\neg P \or Q$ ";

or as the statement of a truth-functional tautology or theorem of propositional logic:

(P \to Q) \to (\neg P \or Q)

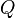where $P$ and $Q$ are propositions expressed in some formal system.

Example

If it is a bear, then it can swim.

Thus, it is not a bear or it can swim.

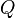where $P$ is the statement "it is a bear" and $Q$ is the statement "it can swim".

If it was found that the bear could not swim, written symbolically as $P \and \neg Q$ , then both sentences are false but otherwise they are both true.

References

↑ Hurley, Patrick (1991). A Concise Introduction to Logic (4th ed.). Wadsworth Publishing. pp. 364–5.
↑ Copi, Irving M.; Cohen, Carl (2005). Introduction to Logic. Prentice Hall. p. 371.