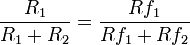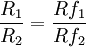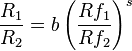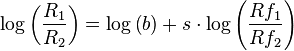Matching law

In operant conditioning, the matching law is a quantitative relationship that holds between the relative rates of response and the relative rates of reinforcement in concurrent schedules of reinforcement. The matching law simply states that there is a correlation between behavior and the environment.[1] It applies reliably when non-human subjects are exposed to concurrent variable interval schedules; its applicability in other situations is less clear, depending on the assumptions made and the details of the experimental situation. This law has significantly helped behaviour analysts lawfully relate behaviour to environment and write equations that clearly show how these two covary.[1]

Stated simply, the matching law suggests that an animal's response rate to a scenario will be proportionate to the amount/duration of reinforcement delivered; behavior ratios are equal to the reinforcer ratios that have been received.

Matching can be applied to single schedule situations because there is always something else a subject can be doing, which means there are other reinforcers in the environment that could be presented, called extraneous reinforcement.

There are three ideas on how humans and animals maximize reinforcement, molecular maximizing, molar maximizing and melioration.

The matching law was first formulated by R.J. Herrnstein (1961) following an experiment with pigeons on concurrent variable interval schedules.[2] Pigeons were presented with two buttons in a Skinner box, each of which led to varying rates of food reward. The pigeons tended to peck the button that yielded the greater food reward more often than the other button; however, they did so at a rate that was similar to the rate of reward.

If R1 and R2 are the rate of responses on two schedules that yield obtained (as distinct from programmed) rates of reinforcement Rf1 and Rf2, the strict matching law holds that the relative response rate R1 / (R1 + R2) matches, that is, equals, the relative reinforcement rate Rf1 / (Rf1 + Rf2). That is,

\frac{R_1}{R_1+R_2}=\frac{Rf_1}{Rf_1+Rf_2}

This relationship can also be stated in terms of response and reinforcement ratios:

\frac{R_1}{R_2}=\frac{Rf_1}{Rf_2}

Subsequent research has shown that data normally depart from strict matching, but are fitted to a very good approximation by a power function generalization of the strict matching (Baum, 1974),

\frac{R_1}{R_2}=b\left(\frac{Rf_1}{Rf_2}\right)^s

This is more conveniently expressed in logarithmic form

\log\left(\frac{R_1}{R_2}\right)=\log\left(b\right)+s\cdot\log\left(\frac{Rf_1}{Rf_2}\right)

The constants b and s are referred to as "bias" and "sensitivity" respectively. Sensitivity changes the slope and bias changes the intercept. This generalized matching law accounts for high proportions of the variance in most experiments on concurrent variable interval schedules in non-humans. Values of b depend on details of the experiment set up, but values of s are consistently found to be around 0.8, whereas the value required for strict matching would be 1.0.[3][4]

The matching law is theoretically important for two reasons. First, it offers a simple quantification of behavior which is capable of extension to a number of other situations. Secondly, it appears to offer a lawful, predictive account of choice; as Herrnstein (1970) expressed it, under an operant analysis, choice is nothing but behavior set into the context of other behavior.[5] It thus challenges any idea of free will, in exactly the way B.F. Skinner had argued that the experimental analysis of behavior should, in his book Beyond Freedom and Dignity. However this challenge is only serious if the scope of the matching law can be extended from pigeons to humans. When human participants perform under concurrent schedules of reinforcement, matching has been observed in some experiments,[6] but wide deviations from matching have been found in others.[7] The matching law has generated a great deal of research, much of it presented to the Society for Quantitative Analysis of Behavior.

There are three deviations from matching: undermatching, overmatching and bias. Undermatching means response proportions are less extreme because a subjects preferences are closer to indifferent than they should be. Undermatching can happen if subjects get in the habit of switching between two options, which can be accidentally reinforced if a reinforcer is given immediately after a subject switches. To reduce the reinforcement of switching, a changeover delay can be used. A changeover delay is a 1.5 second delay when no reinforcer is presented after a switch. Another deviation, the opposite of undermatching, but not as common is overmatching. The subjects response proportions are more extreme than reinforcement proportions. Overmatching may occur if there is a penalty for switching behaviors. The other deviation is bias, which has nothing to do with reinforcement, occurs when subjects spend more time on one alternative than the matching equation predicts, and can happen because subjects prefer a certain environment, area in a laboratory or certain method of responding.

Although Herrstein was the pioneer in this area, a recent review by McDowell reveals that unlike the generalized matching equation, Herrnstein's original equation fails to accurately describe concurrent-schedule data under a substantial range of conditions. Therefore, the generalized matching equation is a much powerful descriptive tool widely used by behaviour analysts.[1]

Role in the development of psychopathology

The matching law greatly expands psychologists' and behavior analysts' understanding of natural phenomena such as development and developmental psychopathology.[8] Response matching has implications for developmental psychopathology research.[9] James Snyder and colleague have found that response matching predicts the use of conflict tactics by children and parents during conflict bouts.[10] This matching rate predicts future arrests. Even children's use of deviant talk appears to follow a matching pattern.[9]

As revealed in a recent and comprehensive review by McDowell (2005), it is clear that whereas the generalized matching equation accurately describes concurrent-schedule data under a substantial range of conditions, Herrnstein's original equation fails to do so.[11]

Notes

  1. ↑ 1.0 1.1 1.2 Poling, A., Edwards, T. L., Weeden, M., & Foster, T. (2011). The matching law. Psychological Record, 61(2), 313-322.
  2. ↑ Herrnstein, R.J. (1961). Relative and absolute strength of responses as a function of frequency of reinforcement. Journal of the Experimental Analysis of Behaviour, 4, 267–72.
  3. ↑ Baum, W.M. (1974). On two types of deviation from the matching law: Bias and undermatching. Journal of the Experimental Analysis of Behavior, 22, 231–42.
  4. ↑ Davison, M. & McCarthy, D. (1988). The matching law: A research review. Hillsdale, NJ: Erlbaum.
  5. ↑ Herrnstein, R.J. (1970). On the law of effect. Journal of the Experimental Analysis of Behavior, 13, 243–66.
  6. ↑ Bradshaw, C.M.; Szabadi, E. & Bevan, P. (1976). Behavior of humans in variable-interval schedules of reinforcement Journal of the Experimental Analysis of Behavior, 26, 135–41.
  7. ↑ Horne, P.J. & Lowe, C.F. (1993). Determinants of human performance on concurrent schedules. Journal of the Experimental Analysis of Behavior, 59, 29–60. doi:10.1901/jeab.1993.59-29
  8. ↑ Strand, P.S. (2001) Momentum, Matching, and Meaning: Toward a Fuller Exploitation of Operant Principles. The Behavior Analyst Today, 2(3), 170–84
  9. ↑ 9.0 9.1 James Snyder, Mike Stoolmiller, Gerald R. Patterson, Lynn Schrepferman, Jessica Oeser, Kassy Johnson, and Dana Soetaert (2003): The Application of Response Allocation Matching to Understanding Risk Mechanisms in Development: The Case of Young Children's Deviant Talk and Play, and Risk for Early-Onset Antisocial Behavior. The Behavior Analyst Today, 4(4), 435–45
  10. ↑ Snyder, J.J. & Patterson, G.R. (1995). Individualized differences in social aggression: A test of the reinforcement hypothesis in the natural environment. Behavior Therapy, 26, 371–91.
  11. ↑ "University of Toronto Libraries Portal". Bf4dv7zn3u.search.serialssolutions.com.myaccess.library.utoronto.ca. 2011-04-01. Retrieved 2011-12-05.

References