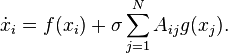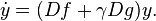Master stability function
In mathematics, the master stability function is a tool used to analyse the stability of the synchronous state in a dynamical system consisting of many identical oscillators which are coupled together, such as the Kuramoto model.
The setting is as follows. Consider a system with  identical oscillators. Without the coupling, they evolve according to the same differential equation, say
identical oscillators. Without the coupling, they evolve according to the same differential equation, say 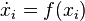 where
where 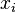 denotes the state of oscillator
denotes the state of oscillator  . A synchronous state of the system of oscillators is where all the oscillators are in the same state.
. A synchronous state of the system of oscillators is where all the oscillators are in the same state.
The coupling is defined by a coupling strength  , a matrix
, a matrix 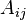 which describes how the oscillators are coupled together, and a function
which describes how the oscillators are coupled together, and a function  of the state of a single oscillator. Including the coupling leads to the following equation:
of the state of a single oscillator. Including the coupling leads to the following equation:
It is assumed that the row sums 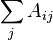 vanish so that the manifold of synchronous states is neutrally stable.
vanish so that the manifold of synchronous states is neutrally stable.
The master stability function is now defined as the function which maps the complex number 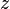 to the greatest Lyapunov exponent of the equation
to the greatest Lyapunov exponent of the equation
The synchronous state of the system of coupled oscillators is stable if the master stability function is negative at 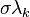 where
where 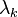 ranges over the eigenvalues of the coupling matrix
ranges over the eigenvalues of the coupling matrix  .
.
References
- Arenas, Alex; Díaz-Guilera, Albert; Kurths, Jurgen; Moreno, Yamir; Zhou, Changsong (2008), "Synchronization in complex networks", Physics Reports 469: 93–153, doi:10.1016/j.physrep.2008.09.002.
- Pecora, Luis M.; Carroll, Thomas L. (1998), "Master stability functions for synchronized coupled systems", Physical Review Letters 80: 2109–2112, doi:10.1103/PhysRevLett.80.2109.