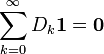Markovian arrival process
In queueing theory, a discipline within the mathematical theory of probability, a Markovian arrival process (MAP or MArP[1]) is a mathematical model for the time between job arrivals to a system. The simplest such process is a Poisson process where the time between each arrival is exponentially distributed.[2][3]
The processes were first suggested by Neuts in 1979.[2][4]
Definition
A Markov arrival process is defined by two matrices D0 and D1 where elements of D0 represent hidden transitions and elements of D1 observable transitions. The block matrix Q below is a transition rate matrix for a continuous-time Markov chain.[5]
The simplest example is a Poisson process where D0 = −λ and D1 = λ where there is only one possible transition, it is observable and occurs at rate λ. For Q to be a valid transition rate matrix, the following restrictions apply to the Di
Special cases
Markov-modulated Poisson process
The Markov-modulated Poisson process or MMPP where m Poisson processes are switched between by an underlying continuous-time Markov chain.[6] If each of the m Poisson processes has rate λi and the modulating continuous-time Markov has m × m transition rate matrix R, then the MAP representation is
Phase-type renewal process
The phase-type renewal process is a Markov arrival process with phase-type distributed sojourn between arrivals. For example if an arrival process has an interarrival time distribution PH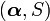 with an exit vector denoted
with an exit vector denoted 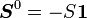 , the arrival process has generator matrix,
, the arrival process has generator matrix,
Batch Markov arrival process
The batch Markovian arrival process (BMAP) is a generalisation of the Markovian arrival process by allowing more than one arrival at a time.[7] The homogeneous case has rate matrix,
An arrival of size 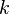 occurs every time a transition occurs in the sub-matrix
occurs every time a transition occurs in the sub-matrix 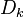 . Sub-matrices
. Sub-matrices 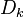 have elements of
have elements of 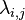 , the rate of a Poisson process, such that,
, the rate of a Poisson process, such that,
and
Fitting
A MAP can be fitted using an expectation–maximization algorithm.[8]
Software
- KPC-toolbox a library of MATLAB scripts to fit a MAP to data.[9]
See also
References
- ↑ Asmussen, S. R. (2003). "Markov Additive Models". Applied Probability and Queues. Stochastic Modelling and Applied Probability 51. pp. 302–339. doi:10.1007/0-387-21525-5_11. ISBN 978-0-387-00211-8.
- ↑ 2.0 2.1 Asmussen, S. (2000). "Matrix-analytic Models and their Analysis". Scandinavian Journal of Statistics 27 (2): 193–226. doi:10.1111/1467-9469.00186. JSTOR 4616600.
- ↑ Chakravarthy, S. R. (2011). "Markovian Arrival Processes". Wiley Encyclopedia of Operations Research and Management Science. doi:10.1002/9780470400531.eorms0499. ISBN 9780470400531.
- ↑ Neuts, Marcel F. (1979). "A Versatile Markovian Point Process". Journal of Applied Probability (Applied Probability Trust) 16 (4): 764–779. JSTOR 3213143. Retrieved 11 June 2013.
- ↑ Casale, G. (2011). "Building accurate workload models using Markovian arrival processes". ACM SIGMETRICS Performance Evaluation Review 39: 357. doi:10.1145/2007116.2007176.
- ↑ Fischer, W.; Meier-Hellstern, K. (1993). "The Markov-modulated Poisson process (MMPP) cookbook". Performance Evaluation 18 (2): 149. doi:10.1016/0166-5316(93)90035-S.
- ↑ Lucantoni, D. M. (1993). "The BMAP/G/1 queue: A tutorial". Performance Evaluation of Computer and Communication Systems. Lecture Notes in Computer Science 729. p. 330. doi:10.1007/BFb0013859. ISBN 3-540-57297-X.
- ↑ Buchholz, P. (2003). "An EM-Algorithm for MAP Fitting from Real Traffic Data". Computer Performance Evaluation. Modelling Techniques and Tools. Lecture Notes in Computer Science 2794. pp. 218–236. doi:10.1007/978-3-540-45232-4_14. ISBN 978-3-540-40814-7.
- ↑ Casale, G.; Zhang, E. Z.; Smirni, E. (2008). "KPC-Toolbox: Simple Yet Effective Trace Fitting Using Markovian Arrival Processes". 2008 Fifth International Conference on Quantitative Evaluation of Systems. p. 83. doi:10.1109/QEST.2008.33. ISBN 978-0-7695-3360-5.
| ||||||||||||||||||||||||||||||||||
![Q=\left[\begin{matrix}
D_{0}&D_{1}&0&0&\dots\\
0&D_{0}&D_{1}&0&\dots\\
0&0&D_{0}&D_{1}&\dots\\
\vdots & \vdots & \ddots & \ddots & \ddots
\end{matrix}\right]\; .](../I/m/5f079744bb42fc530333b5c0261cc99b.png)
![\begin{align}
0\leq [D_{1}]_{i,j}&<\infty \\
0\leq [D_{0}]_{i,j}&<\infty \quad i\neq j \\
\, [D_{0}]_{i,i}&<0 \\
(D_{0}+D_{1})\boldsymbol{1} &= \boldsymbol{0}
\end{align}](../I/m/42c62ed7f9ab786df845be7c164ad13c.png)
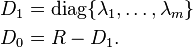
![Q=\left[\begin{matrix}
S&\boldsymbol{S}^{0}\boldsymbol{\alpha}&0&0&\dots\\
0&S&\boldsymbol{S}^{0}\boldsymbol{\alpha}&0&\dots\\
0&0&S&\boldsymbol{S}^{0}\boldsymbol{\alpha}&\dots\\
\vdots&\vdots&\ddots&\ddots&\ddots\\
\end{matrix}\right]](../I/m/aa78d8fe6d6b21dc38b7b3eba2c30b5a.png)
![Q=\left[\begin{matrix}
D_{0}&D_{1}&D_{2}&D_{3}&\dots\\
0&D_{0}&D_{1}&D_{2}&\dots\\
0&0&D_{0}&D_{1}&\dots\\
\vdots & \vdots & \ddots & \ddots & \ddots
\end{matrix}\right]\; .](../I/m/d5c44447beaaad330f707ac95b3e1c4a.png)
![0\leq [D_{k}]_{i,j}<\infty\;\;\;\; 1\leq k](../I/m/9970b234179ec9556cfd5694514e3590.png)
![0\leq [D_{0}]_{i,j}<\infty\;\;\;\; i\neq j](../I/m/9e62b841367c615382a66b6ccf903f5d.png)
![[D_{0}]_{i,i}<0\;](../I/m/7b5f0daa455cecce64459dad793a1bfa.png)