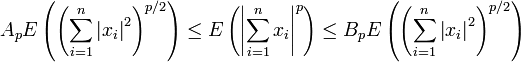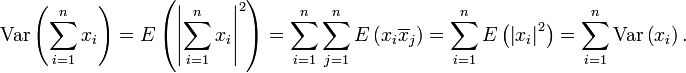Marcinkiewicz–Zygmund inequality
In mathematics, the Marcinkiewicz–Zygmund inequality, named after Józef Marcinkiewicz and Antoni Zygmund, gives relations between moments of a collection of independent random variables. It is a generalization of the rule for the sum of variances of independent random variables to moments of arbitrary order.
Statement of the inequality
Theorem [1][2] If 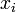 ,
, 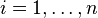 , are independent random variables such that
, are independent random variables such that 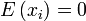 and
and 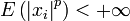 ,
, 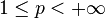 ,
,
where 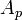 and
and 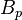 are positive constants, which depend only on
are positive constants, which depend only on 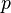 .
.
The second-order case
In the case 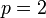 , the inequality holds with
, the inequality holds with 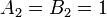 , and it reduces to the rule for the sum of variances of independent random variables with zero mean, known from elementary statistics: If
, and it reduces to the rule for the sum of variances of independent random variables with zero mean, known from elementary statistics: If 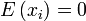 and
and 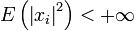 , then
, then
See also
Several similar moment inequalities are known as Khintchine inequality and Rosenthal inequalities, and there are also extensions to more general symmetric statistics of independent random variables.[3]
Notes
- ↑ J. Marcinkiewicz and A. Zygmund. Sur les foncions independantes. Fund. Math., 28:60–90, 1937. Reprinted in Józef Marcinkiewicz, Collected papers, edited by Antoni Zygmund, Panstwowe Wydawnictwo Naukowe, Warsaw, 1964, pp. 233–259.
- ↑ Yuan Shih Chow and Henry Teicher. Probability theory. Independence, interchangeability, martingales. Springer-Verlag, New York, second edition, 1988.
- ↑ R. Ibragimov and Sh. Sharakhmetov. Analogues of Khintchine, Marcinkiewicz–Zygmund and Rosenthal inequalities for symmetric statistics. Scandinavian Journal of Statistics, 26(4):621–633, 1999.