Mapping cylinder
In mathematics, specifically algebraic topology, the mapping cylinder of a function  between topological spaces
between topological spaces  and
and  is the quotient
is the quotient
where the union is disjoint, and ∼ is the equivalence relation generated by
That is, the mapping cylinder 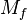 is obtained by gluing one end of
is obtained by gluing one end of ![X\times[0,1]](../I/m/7ff959d5b1233da08ed4a5475eb52233.png) to
to  via the map
via the map  . Notice that the "top" of the cylinder
. Notice that the "top" of the cylinder 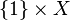 is homeomorphic to
is homeomorphic to  , while the "bottom" is the space
, while the "bottom" is the space 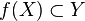 .
.
See [1] for more details.
Basic properties
The bottom Y is a deformation retract of 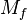 .
The projection
.
The projection 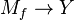 splits (via
splits (via 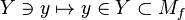 ), and a deformation retraction
), and a deformation retraction  is given by:
is given by:
(where points in  stay fixed, which is well-defined, because
stay fixed, which is well-defined, because ![[0,x]=[s\cdot 0,x]](../I/m/50a0d3e44bcb8ee66b9708e074955ed7.png) for all
for all  ).
).
The map 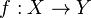 is a homotopy equivalence if and only if the "top"
is a homotopy equivalence if and only if the "top" 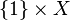 is a strong deformation retract of
is a strong deformation retract of 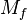 . A proof can be found in.[2] An explicit formula for the strong deformation retraction is produced in.[3]
. A proof can be found in.[2] An explicit formula for the strong deformation retraction is produced in.[3]
Interpretation
The mapping cylinder may be viewed as a way to replace an arbitrary map by an equivalent cofibration, in the following sense:
Given a map 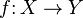 , the mapping cylinder is a space
, the mapping cylinder is a space 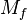 , together with a cofibration
, together with a cofibration 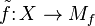 and a surjective homotopy equivalence
and a surjective homotopy equivalence 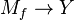 (indeed, Y is a deformation retract of
(indeed, Y is a deformation retract of 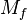 ), such that the composition
), such that the composition 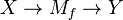 equals f.
equals f.
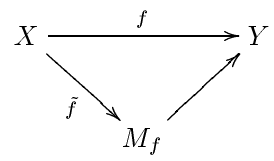
Thus the space Y gets replaced with a homotopy equivalent space 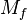 , and the map f with a lifted map
, and the map f with a lifted map 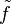 . Equivalently, the diagram
. Equivalently, the diagram
gets replaced with a diagram
together with a homotopy equivalence between them.
The construction serves to replace any map of topological spaces by a homotopy equivalent cofibration.
Note that pointwise, a cofibration is a closed inclusion.
Applications
Mapping cylinders are quite common homotopical tools. One use of mapping cylinders is to apply theorems concerning inclusions of spaces to general maps, which might not be injective.
Consequently, theorems or techniques (such as homology, cohomology or homotopy theory) which are only dependent on the homotopy class of spaces and maps involved may be applied to 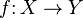 with the assumption that
with the assumption that 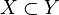 and that
and that  is actually the inclusion of a subspace.
is actually the inclusion of a subspace.
Another, more intuitive appeal of the construction is that it accords with the usual mental image of a function as "sending" points of  to points of
to points of 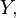 and hence of embedding
and hence of embedding  within
within 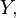 despite the fact that the function need not be one-to-one.
despite the fact that the function need not be one-to-one.
Categorical application and interpretation
One can use the mapping cylinder to construct homotopy limits: given a diagram, replace the maps by cofibrations (using the mapping cylinder) and then take the ordinary pointwise limit (one must take a bit more care, but mapping cylinders are a component).
Conversely, the mapping cylinder is the homotopy pushout of the diagram where 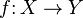 and
and 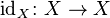 .
.
Mapping telescope
Given a sequence of maps
the mapping telescope is the homotopical direct limit. If the maps are all already cofibrations (such as for the orthogonal groups 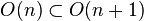 ), then the direct limit is the union, but in general one must use the mapping telescope. The mapping telescope is a sequence of mapping cylinders, joined end-to-end. The picture of the construction looks like a stack of increasingly large cylinders, like a telescope.
), then the direct limit is the union, but in general one must use the mapping telescope. The mapping telescope is a sequence of mapping cylinders, joined end-to-end. The picture of the construction looks like a stack of increasingly large cylinders, like a telescope.
Formally, one defines it as
See also
- Mapping cylinder (homological algebra)
References
- Aguado, A. (2012). "A Short Note on Mapping Cylinders".
- Hatcher, A. (2002). Algebraic Topology. Cambridge University Press. ISBN 0-521-79540-0.
- May, J.P (1999). A Concise Course in Algebraic Topology. The University of Chicago Press. ISBN 978-0-2265-1183-2.
![M_f = (([0,1]\times X) \amalg Y)\,/\,\sim](../I/m/d6f2510b8f305a97a11031efe09a45ce.png)
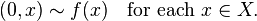
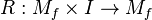
![([t,x],s) \mapsto [s\cdot t,x]](../I/m/9f30aa9c089b39bd89760e9afefee57b.png)

![\Bigl(\coprod_i [0,1] \times X_i\Bigr) / ((0,x_i) \sim (1,f(x_i)))](../I/m/6c9ae07c11c3471af6ec5d30606492e0.png)