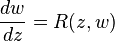Malmquist's theorem

In mathematics, Malmquist's theorem, introduced by Axel Johannes Malmquist (1913, 1920, 1941), is a theorem restricting the differential equations that have meromorphic solutions.

Statement

Malmquist's theorem states that if w is a meromorphic function with infinitely many poles satisfying the complex differential equation

where R(z,w) is a rational function, then as a function of w, R is a polynomial of degree 2; in other words the differential equation is a Riccati equation.

References

• Malmquist, J. (1913), "Sur les fonctions a un nombre fini de branches définies par les équations différentielles du premier ordre", Acta Mathematica 36 (1): 297–343, doi:10.1007/BF02422385 
• Malmquist, J. (1920), "Sur les fonctions a un nombre fini de branches définies par les équations différentielles du premier ordre", Acta Mathematica 42 (1): 317–325, doi:10.1007/BF02404413 
• Malmquist, J. (1941), "Sur les fonctions a un nombre fini de branches définies par les équations différentielles du premier ordre", Acta Mathematica 74 (1): 175–196, doi:10.1007/BF02392253, MR 0005974