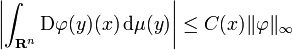Malliavin's absolute continuity lemma

In mathematics — specifically, in measure theory — Malliavin's absolute continuity lemma is a result due to the French mathematician Paul Malliavin that plays a foundational rôle in the regularity (smoothness) theorems of the Malliavin calculus. Malliavin's lemma gives a sufficient condition for a finite Borel measure to be absolutely continuous with respect to Lebesgue measure.

Statement of the lemma

Let μ be a finite Borel measure on n-dimensional Euclidean space Rn. Suppose that, for every x ∈ Rn, there exists a constant C = C(x) such that

\left| \int_{\mathbf{R}^{n}} \mathrm{D} \varphi (y) (x) \, \mathrm{d} \mu(y) \right| \leq C(x) \| \varphi \|_{\infty}

for every C∞ function φ : Rn → R with compact support. Then μ is absolutely continuous with respect to n-dimensional Lebesgue measure λn on Rn. In the above, Dφ(y) denotes the Fréchet derivative of φ at y and ||φ||∞ denotes the supremum norm of φ.

References