Magnetospheric electric convection field

^[1]The impact of the solar wind onto the magnetosphere generates an electric field within the inner magnetosphere (r < 10 a; with a the Earth's radius) - the convection field-. Its general direction is from dawn to dusk. The co-rotating thermal plasma within the inner magnetosphere drifts orthogonal to that field and to the geomagnetic field B_o. The generation process is not yet completely understood.^[2] One possibility is viscous interaction between solar wind and the boundary layer of the magnetosphere (magnetopause). Another process may be magnetic reconnection. Finally, a hydromagnetic dynamo process in the polar regions of the inner magnetosphere may be possible. Direct measurements via satellites have given a fairly good picture of the structure of that field.^[3][4][5] A number of models of that field exists.^[6][7][8][9]

A widely used model is the Volland-Stern model ^{[10][11] [12]}

Model Description

It is based on two simplifying assumptions: first, a coaxial geomagnetic dipole field B is introduced. Its magnetic field lines can be represented by the shell parameter

(1)   L=r/[a sin²θ]

with r the distance from the Earth, a the Earth's radius, and θ the co-latitude. For r = a, θ is the co-latitude of the foot point of the line on the ground. L = const is the equation of a magnetic field line, and r = a L is the radial distance of the line at the geomagnetic equator (θ = 90°). Second, it is assumed that the electric field can be derived from an electrostatic potential Φ_c. Since in a highly conducting electric plasma like the magnetosphere, the electric fields must be orthogonal to the magnetic fields, the electric potential shell is parallel to the magnetic shell. The relation

(2)   Φ_c = [Φ_co/2] (L/L_m)^q sin(τ -τ_co)

fulfills that condition. Here L_m = 1/sin²θ_m is the separatrix^[13] separating the low latitude magnetosphere with closed geomagnetic field lines at θ ≥ θ_m from the polar magnetosphere with open magnetic fieldlines (having only one footpoint on Earth), and τ the local time. θ_m ~ 20° is the polar border of the auroral zone. q, Φ_co, and τ_co are empirical parameters, to be determined from the observations. Eq.(2) yields for a coordinate system co-rotating with the Earth, its geomagnetic equator being identical with the geographic equator. Since the electric potential is symmetric with respect to the equator, only the northern hemisphere needs to be considered. The general direction of the potential is from dawn to dusk, and Φ_co is the total potential difference. For a transformation from a rotating magnetospheric coordinate system into a non-rotating system, τ must be replaced by the longitude -λ.

Inner Magnetosphere

With the numbers q ~ 2, and Φ_co and τ_co increasing with geomagnetic activity (e.g., Φ_co ~ 17 and 65 kVolt, and τ_co ~ 0 and 1 h, during geomagnetically quiet and slightly disturbed conditions, respectively), eq. (2) valid at lower latitudes, (θ > θ_m) and within the inner magnetosphere (r ≤ 10 a) is the Volland-Stern model (see Fig. 1 a)).

Figure 1: Equipotential lines of electric convection field within the equatorial plane of the magnetosphere (left), and superposition of the convection field with the co-rotation field (right) during magnetically quiet conditions

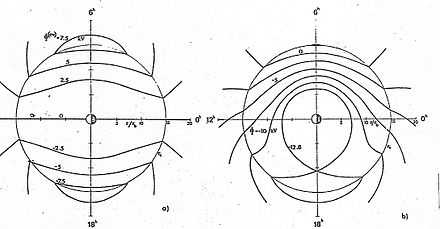
The use of an electrostatic field means that this model is valid only for slow temporal variations (of the order of one day are larger). The assumption of a coaxial magnetic dipole field implies that only global scale structures can be simulated. The electric field components are derived from

(3)   E = - grad Φ

as

E_r = - (q/r)Φ_c
E_θ = (2q/r) cotθ Φ_c
E_λ = - 1/(r sinθ) cot(λ - λ_co) Φ_co

In the presence of the geomagnetic field an electric field is generated in a rotating on frame of reference in order to compensate for the Lorentz force. This is the so-called electric co-rotation field measured by an observer rotating with the Earth. With the simplifying conditions give above its potential is

(4)   Φ_r = - Φ_ro/L

with Φ_ro = 90 kVolt. The thermal plasma within the inner magnetosphere co-rotates with the Earth. In a non-rotating frame of reference, it reacts to the sum of both fields

(5)   Φ_c + Φ_r

in eq.(2) and (4). Since Φ_r decreases with distance from the Earth while Φ_c increases, the configuration of the sum of both potentials has a torus-like inner region of closed equipotential shells, called the plasmasphere, in which ionized particles of thermal energy remain trapped (e.g.,^[14]). Indeed, whistler observations have revealed a plasma density within the plasmasphere several orders of magnitude larger than outside the plasmapause, which is the last closed equipotential shell ^[15] (see Fig. 1b)). From the shape of the observed plasmapause configuration, the exponent q = 2 in eq.(2) has been determined, while the extent of the plasmapause decreasing with geomagnetic activity is simulated by the amplitude Φ_co

Origin of Convection Field

The origin of the electric convection field results from the interaction between the solar wind plasma and the geomagnetic field. In the polar regions with open magnetic field lines (where the geomagnetic field merges with the interplanetary magnetic field), the solar wind flowing through the polar magnetosphere induces an electric field directed from dawn to dusk. Charge separation takes place at the magnetopause. This area is connected via the last closed shell parameter L_m with the ionospheric dynamo region. Thus, discharging currents flow via electric field-aligned currents (Birkeland currents) along L_m within the ionospheric dynamo region.^[16] The field-aligned currents flow into the ionosphere on the morning side and out of the ionosphere on the evening side. The variability of the solar wind flux determines the magnetospheric activity, generally expressed by the degree of geomagnetic activity observed on the ground.

Polar Magnetosphere

The electric convection field in the near Earth polar region can be simulated by eq. (2) with the exponent q = - 1/2.^[10] At the separatrix at L_m ,Φ_c is continuous. However, a field reversal takes place accompanied by field-aligned currents, both in agreement with the observations.^[4][5] The electric field reversal at L_m clearly indicates a reversal of the plasma drift within the inner and the polar magnetosphere. In a more sophisticated model,^[16] the auroral oval between about 15° and 20°colatitude (again simulated by a coaxial auroral zone), as a transition zone between the field reversal, has been taken into account. The ionospheric dynamo region between about 100 to 200 km altitude is a region where ions and electrons have different mobility. Thus the plasma becomes electrically conducting. Due to the geomagnetic field, two kinds of electric currents exist: Pedersen currents parallel to E, and Hall currents orthogonal to E and B. Moreover, a significant enhancement of the electric conductivity within the aurora area depending on geomagnetic activity exists which influences the parameter τ_co in eq.(2)

The electric convection field drives strong electric currents within the polar dynamo regions (e.g. DP1 and DP2) which can be simulated by the model. Manifestations of upper atmospheric electric currents are the corresponding magnetic variations on the ground. Unfortunately, this connection is unique only for horizontally flowing current systems. E.g., the vertically flowing field-aligned currents have almost no magnetic effect on the ground.^[17] The model allows to separate the contributions of both kinds of electric currents. The polar magnetic disturbances DP2 are mainly Hall currents. The auroral electrojets (DP1) with magnitudes of the order of several hundreds of kA flowing within the aurora zones consist of Hall currents and Pedersen currents. Dissipation of the Pedersen currents produces Joule heating which is transferred to the neutral gas of the thermosphere thus generating thermospheric and ionospheric disturbances. Longer-lasting magnetospheric disturbances of the order of several hours to days can develop into global-scale thermospheric and ionospheric storms (e.g.,^[18]).

Literature