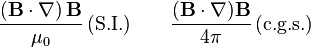Magnetic tension force

The magnetic tension force is a restoring force (SI unit: Pa·m−1) that acts to straighten bent magnetic field lines. It equals:

\frac{\left(\mathbf{B}\cdot\nabla\right)\mathbf{B}}{\mu_0} \, (\text{S.I.}) \qquad \frac{(\mathbf B\cdot\nabla)\mathbf B}{4\pi} \,(\text{c.g.s.})

It is analogous to rubber bands and their restoring force. The force is directed antiradially. Although magnetic tension is referred to as a force, it is actually a pressure gradient (Pa m−1) which is also a force density (N m−3).

The magnetic pressure is the energy density of the magnetic field and it increases as magnetic field lines convene with each other. In contrast, magnetic tension force is determined by how much the magnetic pressure changes with distance. Magnetic tension forces also rely on vector current densities 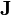\mathbf{J} and their interaction with the magnetic field 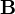\mathbf{B}. 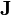Plotting magnetic tension along adjacent field lines can give a picture as to their divergence and convergence with respect to each other as well as current densities \mathbf{J}.

Use in Plasma Physics

Magnetic tension is particularly important in plasma physics and magnetohydrodynamics, where it controls dynamics of some systems and the shape of magnetized structures. In magnetohydrodynamics, the magnetic tension force can be derived from the momentum equation of plasma physics:

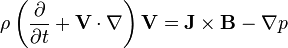\rho\left(\frac{\partial}{\partial t}+ \mathbf{V}\cdot\nabla \right)\mathbf{V} = \mathbf{J}\times\mathbf{B} - \nabla p .

The first term on the right hand side of the above equation represents electromagnetic forces and the second term represents pressure gradient forces. Using the relation 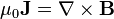\mu_0\mathbf{J}=\nabla\times\mathbf{B} and the vector identity

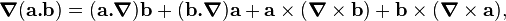
 \boldsymbol{\nabla}(\textbf{a.}\textbf{b})=(\textbf{a.}\boldsymbol{\nabla})\textbf{b}+(\textbf{b.}\boldsymbol{\nabla})\textbf{a}+\textbf{a}\times(\boldsymbol{\nabla}\times\textbf{b})+\textbf{b}\times(\boldsymbol{\nabla}\times\textbf{a}),

we obtain the following equation:

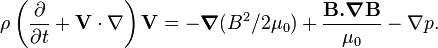
\rho\left(\frac{\partial}{\partial t}+ \mathbf{V}\cdot\nabla \right)\mathbf{V} =-\boldsymbol{\nabla}(B^2/2\mu_0) + {\textbf{B.}\boldsymbol{\nabla}\textbf{B} \over \mu_0} - \nabla p.

The first and last gradient terms are associated with the total pressure which is the sum of the magnetic and thermal pressures; 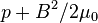p+B^2/2\mu_0. The second term represents the magnetic tension.

See also

References