Magnetic dipole transition

The interaction of an electromagnetic wave with an electron bound in an atom or molecule can be described by time-dependent perturbation theory. Magnetic dipole transitions describe the dominant effect of the coupling to the magnetic part of the electromagnetic wave. They can be divided into two groups by the frequency at which they are observed: Optical magnetic dipole transitions can occur at frequencies in the infrared, optical or ultraviolet between sublevels of two different electronic levels, Magnetic Resonance transitions can occur at microwave or radio frequencies between angular momentum sublevels within a single electronic level. The latter are called Electron Paramagnetic Resonance (EPR) transitions if they are associated with the electronic angular momentum of the atom or molecule and Nuclear Magnetic Resonance (NMR) transitions if they are associated with the nuclear angular momentum.^[1]

Theoretical description

The Hamiltonian of an electron bound in an atom interacting with an electromagnetic field is given by (the theoretical description follows ^[2]):

$H=\frac{1}{2m}[\mathbf{P}-q\mathbf{A}(\mathbf{R},t)]^2+V(R)-\frac{q}{m}\mathbf{S} \cdot \mathbf{B}(\mathbf{R},t)$

The Hamiltonian can be split into a time independent and a time dependent part:

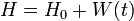
$H=H_0+W(t)$

with

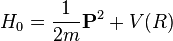
$H_0=\frac{1}{2m} \mathbf{P}^2 +V(R)$

the atomic Hamiltonian and the interaction with the electromagnetic wave (time-dependent):

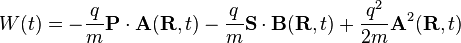
$W(t)=-\frac{q}{m} \mathbf{P}\cdot \mathbf{A}(\mathbf{R},t)-\frac{q}{m} \mathbf{S}\cdot \mathbf{B}(\mathbf{R},t)+\frac{q^2}{2m} \mathbf{A}^2(\mathbf{R},t)$

Since the last term is quadratic in A it can be neglected for small fields. The time-dependent part can be expanded in terms belonging to electric dipole, magnetic dipole, electric quadropole and higher order terms. The term belonging to the magnetic dipole transitions is:

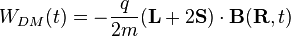
$W_{DM}(t)=-\frac{q}{2m} (\mathbf{L}+2\mathbf{S})\cdot\mathbf{B}(\mathbf{R},t)$

Selection rules

The selection rules for allowed magnetic dipole transitions are:

1. 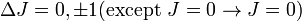$\Delta J=0,\pm 1 (\text{except } J=0 \rightarrow J=0)$ (J: total angular momentum quantum number)

2. $\Delta M_J=0,\pm 1$ ( $M_J$ : projection of the total angular momentum along a specified axis)

3. No parity change

Comparison to electric dipole transitions

Electric dipole transitions only have a non-vanishing matrix element between quantum states with different parity. Magnetic dipole transitions and electric quadrupole transitions in contrast couple states with the same parity.^[1]
The response of these two transitions is much weaker than that of electric dipole transitions.
The electronic states of atoms and molecules normally don't have a static electric dipole moment but many states have a static magnetic dipole moment. The classical magnetized top model can be used to describe magnetic resonances for atoms with static magnetic dipole moment between different Zeeman-split-sublevel in a sufficient way without needing a full quantum mechanical description.^[2]

References

↑ 1.0 1.1 C.Cohen Tannoudji; B.Diu; F.Laloe (1999). Quantum mechanics. Wiley. ISBN 978-0-471-56952-7.
↑ 2.0 2.1 A. E. Siegman (1986). LASERS. University Science Books. ISBN 0-935702-11-3.

External links

National Institute of Standards and Technology